Полный дифференциал и его вычисление

Теорема (о полном дифференциале). Для того чтобы выражение 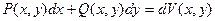- было полным дифференциалом некоторой функции - потенциала, необходимо и достаточно, чтобы в условиях формулы Грина было выполнено одно из следующих четырех условий (эквивалентных условий полного дифференциала)

1) 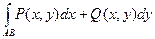зависит только от начальной A и конечной B точек дуги 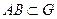и не зависит от формы дуги (не зависит от пути интегрирования),

2) 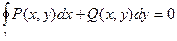для любого кусочно-гладкого контура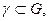

3) ,

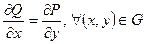4) .

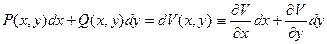Доказательство. Схема доказательства теоремы 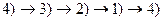. По этой цепочке можно последовательно добраться от любого пункта к любому другому.

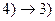Дополнительно предположим, что существуют и непрерывны вторые смешанные производные функции V. Тогда они равны.

.

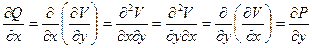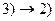. Это следует из формулы Грина.

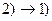. Пусть точки A, B соединены двумя дугами L₁ и L₂. Тогда из них можно составить контур 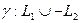, интеграл вдоль которого по п.2 равен нулю.

== -

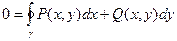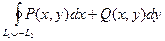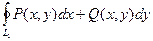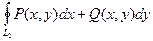. Поэтому =.

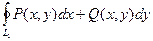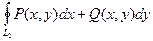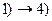. Докажем, что 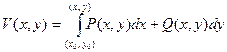- потенциал, то есть, что

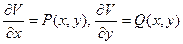. Докажем первое соотношение, второе доказывается аналогично.

=

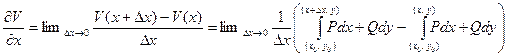Заметим, что такая запись интеграла показывает, что интеграл не зависит от формы дуги. Поэтому мы можем в первом интеграле провести дугу через точку (x, y), чтобы в первом и втором интеграле сократились интегралы по дуге, соединяющей начальную точку с точкой (x, y). В первом интеграле выберем в качестве дуги, соединяющей точку (x, y) с точкой (x+Dx) отрезок прямой, параллельный оси OX. На этом отрезке y не изменяется, поэтому dy=0

Тогда, продолжая равенство, получим

= =

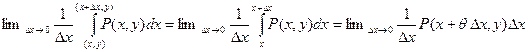(здесь мы перешли от криволинейного интеграла к определенному, так как дуга интегрирования – отрезок, параллельный оси OX и применили теорему о среднем для определенного интеграла). Теперь используем непрерывность функции P(x, y) по переменной x.

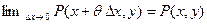= . Первое соотношение доказано.

Для доказательства второго соотношения варьируется переменная y, дуга, соединяющая точки (x_0, y₀), и (x, y+Dy) проводится через точку (x, y) и далее по отрезку, параллельному оси OY, соединяющему точки (x, y) и (x, y+Dy).

Формула Ньютона – Лейбница.

Пусть выполнены условия теоремы о полном дифференциале и пусть выражение

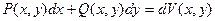- полный дифференциал, а функция - потенциал.

Тогда справедлива формула Ньютона – Лейбница

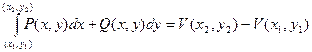, где - потенциал.

Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде 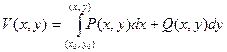. Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x₁, y₁), (x₂, y₂) можно провести через точку (x₀, y₀). Поэтому =+ = - = .

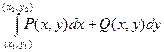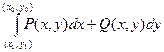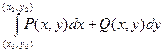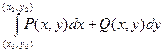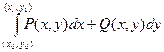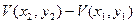Дата добавления: 2014-01-20