Поверхностный интеграл второго рода

Поверхность называется ориентируемой, если в каждой ее точке существует вектор нормали к , - непрерывная вектор – функция на .

Поверхность называется односторонней, если при обходе поверхности по контуру g вектор нормали меняет свое направление на противоположное.

Поверхность называется двусторонней, если при обходе поверхности по контуру g вектор нормали не меняет свое направление.

Примером односторонней поверхности является петля Мебиуса, примерами двусторонних поверхностей – плоскость, сфера, гиперболоиды и т.д.

Задача о потоке жидкости через поверхность.

Поток жидкости через поверхность .– это количество жидкости, протекающее через поверхность в единицу времени.

Пусть на элементе поверхности площадке в некоторой ее точке M проведен вектор 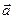перемещения частицы жидкости через площадку в единицу времени. Предполагаем, что для всех точек перемещение одинаково по величине и направлению. Поток жидкости можно вычислить как объем наклонного (по направлению вектора перемещений) параллелепипеда, построенного на . Этот объем равен , где 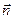- единичный вектор нормали к поверхности. Тогда поток жидкости равен П =

Здесь мы вычисляли дифференциал потока, а затем интегрировали по всей поверхности – это метод дифференциалов при построении интеграла.

Можно строить интеграл с помощью метода интегральных сумм, как мы действовали обычно.

- Введем разбиение области на элементы так, чтобы соседние элементы не содержали общих внутренних точек (условие А),

- на элементах разбиения отметим точку М. Предполагая перемещение частиц жидкости постоянным на элементе и равным 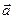(M), вычислим приближенно поток через элемент разбиения и просуммируем его по элементам, получая интегральную сумму .

- Измельчим разбиение при условии (условие В) и перейдем к пределу получая поверхностный интеграл второго рода

.

По виду это – поверхностный интеграл первого рода, он и имеет те же свойства, что поверхностный интеграл первого рода, но имеет еще и свойство ориентируемости. Интеграл по внешней стороне поверхности отличается знаком от интеграла по внутренней стороне поверхности, так как на различных сторонах поверхности нормали в той же точке нормали направлены по одной прямой в различные стороны.

Теорема существования формулируется так же, как для поверхностного интеграла первого рода с тем же замечанием о независимости интеграла от способа выбора разбиения (лишь бы выполнялись условия А), от выбора точек на элементах разбиения, от способа измельчения разбиения (лишь бы выполнялось условие В).

Дата добавления: 2014-01-20