Электрические характеристики

Каждый из радиоматериалов обладает электрическими свойствами, т.к. все радиоматериалы (в том числе и диэлектрики) обладают электро-проводностью. Для оценки электрических свойств используются электрические характеристики.

Удельное электрическое сопротивление ρ – это электрическая харак-теристика, применяемая для оценки электропроводности материалов. Она выражается в омах на метр (Ом·м). В радиоэлектронике используют также меньшую единицу (Ом·см). Для оценки большой электропроводности металлических проводниковых материалов (меди, алюминия и др.) применяют еще меньшую величину удельного электрического сопротивле-ния – микроом на метр (мкОм·м). Соотношение между перечисленными единицами: 1 Ом·см = 10 000 мкОм·м = 0,01 Ом·м.

Все радиоматериалы по эдектропроводности можно разделить на три основные группы:

проводники ρ = 10^-8 ÷ 10^-5 Ом·м,

полупроводники ρ = 10^-6 ÷ 10⁷ Ом·м,

диэлектрики ρ = 10⁷ ÷ 10¹⁸ Ом·м.

Удельное электрическое сопротивление любого радиоматериала зависит от температуры, (рисунок 1.1-а). Так у проводников с повышением температуры удельное электрическое сопротивление возрастает. Это связано с более интенсивным колебанием атомов в узлах кристаллической решетки проводника, что мешает направленному перемещению свободных электронов. У полупроводников и диэлектриков, наоборот, с возрастанием температуры удельное электрическое сопротивление уменьшается. Это объясняется увеличением концентрации носителей электрических зарядов.

а)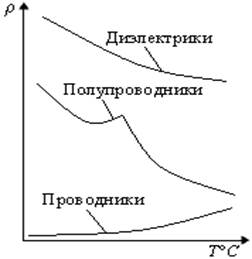 б)

Рисунок 1.1 – Зависимость удельного электрического сопротивления мате-риалов от температуры (а), токи объемной и поверхностной электропро-водности в диэлектрике (б).

Температурный коэффициент удельного сопротивления ТК ρ – величи-на, с помощью которой можно учитывать изменение удельного электричес-кого сопротивления в зависимости от температуры материала. при линейном изменении удельного сопротивления, что наблюдается в сравнительно узких интервалах температур ТК ρ (К^-1) определяется по формуле

ТК ρ = (ρ ₂ – ρ ₁) / ρ ₁(Т ₂ – Т ₁),

где ρ ₁ и ρ ₂ - удельные сопротивления материала при начальной Т ₁ и конечной Т ₂ температурах.

У проводников с ростом температуры удельное сопротивление возрастает, т.е. ТК ρ > 0 – положительная величина, у полупроводников и диэлектриков с ростом температуры удельное сопротивление уменьшается, т.е. ТК ρ < 0 – величина отрицательная.

В твердых диэлектриках имеются токи объёмной I_V и поверхностной I_S электропроводности (рисунок 1.1-б), поэтому у них определяют удельное объёмное ρ _V и поверхностное ρ _S сопротивления. Удельное поверхностное сопротивление так же как и общее, выражается в омах. Удельное объёмное сопротивление характеризует свойство диэлектрика проводить ток через свой объём, а удельное поверхностное сопротивление – по своей поверх-ности. У диэлектриков ρ _V = 10⁷÷ 10¹⁸ Ом·м; ρ _S = 10⁹ ÷ 10¹⁶ Ом.

Поскольку проводники и полупроводники хорошо проводят ток, разделять токи объёмной и и поверхностной электропроводности невоз-можно, поэтому у них определяют общее удельное сопротивление ρ.

Удельная проводимость γ (См /м) – величина, обратная удельному сопротивлению γ = 1/ ρ.

У твердых диэлектриков различают удельную объёмную γ _V = 1/ ρ _V

(См /см, Ом^-1·м^-1)и удельную поверхностную проводимости γ _S = 1/ ρ_S (См).

Удельной проводимостью характеризуется степень электропровод-ности радиоматериала. Так, у проводников γ = 10⁵ ÷ 10⁸ См/м, а у полупроводников γ = 10⁶ ÷ 10^-7 См/м. Удельные объёмная и поверхностная проводимости твердых диэлектриков очень малы: γ _V = 10^-7 ÷ 10^-18 См/м,

γ _S = 10^-8÷ 10^-16 См. Это позволяет использовать их для изоляции частей радиоэлектронных устройств, находящихся под разными электрическими потенциалами.

Для оценки электрического сопротивления тонких пленок (диэлектриков, полупроводников и др.), напримерв в тонкопленочных инте-гральных микросхемах, используют сопротивление пленки R _ (Ом /_), отне-сенное к квадрату её поверхности (рисунок 1.2-а): R _ = ρ а /Δ а = ρ/Δ.

а) б)

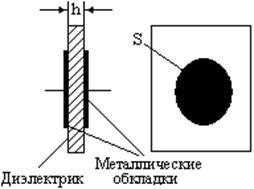
Рисунок 1.2 – Измерение электрического сопротивления тонких пленок (а), плоский конденсатор (б).

Из приведенного выражения следует, что R _ зависит от удельного электрического сопротивления ρ материала пленки и её толщины Δ. Во мно-гих случаях, когда трудно непосредственно измерить толщину пленки, используют электрическую характеристику (параметр) R _ .

Диэлектрическая проницаемость ε_r (относительная диэлектрическая проницаемость) характеризует способность диэлектрика или полупроводника образовывать электрическую емкость. Емкость С (Ф) плос-го конденсатора (рисунок 1.2-б) заданных размеров прямо пропорциональна диэлектрической проницаемости применяемого в нем диэлектрика С = ε_аS/h, где ε_а – абсолютная диэлектрическая проницаемость, Ф/м, S – площадь одной металлической обкладки, м², h – толщина диэлектрика, м; ε_а = ε₀ ε_r, где ε₀ = 8,85416·10^-12 – электрическая постоянная, Ф/м, ε_r – относительная диэлектрическая проницаемость (безразмерная величина). Наименьшую диэ-лектрическую проницаемость имеет вакуум (ε_r = 1), жидкие и твердые диэле- ктрики (ε_r ≈ 2÷17); диэлектрическая проницаемость воздуха ε_r = 1,00058.

Диэлектрическая проницаемость некоторых твердых (активных) диэле-ктриков, называемых сегнетоэлектриками, при комнатной температуре дос-тигает очень больших значений (ε_r = 1500÷7500). Это позволяет изготовлять из них конденсаторы очень малых размеров.

Температурный коэффициент диэлектрической проницаемости ТК ε_r (К^-1) характеризует изменение диэлектрической проницаемости ε_r ра-диоматериалов от температуры (рисунок 1.3-а):

ТКε_r = (ε_r1 - ε_r2) /ε_r1 (Т₁ - Т₂), где ε_{r 1} и ε_{r 2} - диэлектрическая прони-цаемость материала при начальной Т₁ и при конечной Т₂ температурах. Температурный коэффициент диэлектрической проницаемости имеет положительное или отрицательное значение и соответственно указывает, возрастает или убывает (при увеличении температуры) диэлектрическая проницаемость данного диэлектрика.

Тангенс угла диэдектрических потерь tgδ характеризует активные по-тери энергии, рассеиваемые в диэлектрике при его работе в переменном электрическом поле. Из электротехники известно, что мощность, выде-ляемые в проводнике, подключенном в цепь постоянного тока Р ₌ , и мощ-ность при его подключении в цепь переменного тока Р _~ будут одинаковыми, если действующее значение переменного тока будет равно значению постоянного Р₌ = Р _~.

Если же диэлектрик один раз включить под постоянное напряжение, а другой – под переменное, мощность, выделяемая в диэлектрике, включенном под переменное напряжение, будет значительно больше мощности, теряемой при включении его под постоянное напряжение Р_~ > Р₌.

Неравенство потерь энергии наблюдается только в диэлектриках. По-тери мощности в диэлектриках, работающих в электрических полях, назы-вают диэлектрическими потерями. В диэлектрике, включенном под посто-янное напряжение, протекает только активный ток – ток проводимости I_пр. В этом случае активная мощность (Вт), теряемая в диэлектрике, Р = U I_пр.

В диэлектрике, работающем под переменным напряжением, проходят три тока, сдвинутые по фазе (по времени): смещения I_см, абсорбции I_абс, и проводимости I_пр. Эти токи и напряжение U, приложенное к диэлектрику, изображены в виде векторной диаграммы на рисунках 1.3-б.

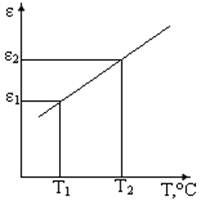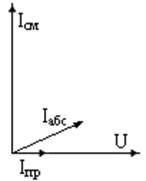а) б) в)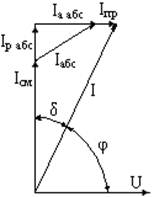

Рисунок 1.3 – Зависимость диэлектрической проницаемости от температуры (а), векторное изображение токов (б), сложение токов в диэлектрике (в).

Напряжение на векторной диаграмме изображено в виде горизонтального вектора U. Ток смещения I_см опережает напряжение на 90°, ток абсорбции тоже опережает напряжение по фазе, но меньше, чем на 90°, а ток проводимости I_пр совпадает по фазе с напряжением. На рисунке 1.3-в показан общий ток I в диэлектрике, полученный сложением векторов всех трех токов. Угол между вектором напряжения U и вектором общего тока I обозначают буквой φ и называют углом сдвига фаз. Угол между вектором общего тока I и вектором тока смещения I_см обозначают буквой δ и называют углом диэлектрических потерь.

Вектор тока абсорбции I_абс разложим на активную I_{А абс} и реактивную

I_{Р абс} составляющие. Сумма токов проводимости I_пр и активной составляющей тока абсорбции I_{А абс} является активной составляющей I_А общего тока I в диэлектрике, т.е. I_А = I_пр + I_{А абс}.

Сумма токов смещения I_см и реактивной составляющей тока абсор-бции I_{Р абс} представляет собой реактивную составляющую I_Р общего тока I, т.е. I_Р = I_см + I_{Р абс}.

Активная мощность (Вт), рассеиваемая в диэлектрике (конденсаторе), равна произведению напряжения, приложенного к конденсатору, на сумму активных токов Р_А = U I_А. Реактивная мощность (В·А) равна произведению приложенного напряжения на сумму реактивных токов Р_Р = U I_Р.

Из векторной диаграммы токов находим I_А / I_Р = tgδ, как известно реактивный (емкостный) ток I_Р = U ωC, отсюда находим выражение для активного тока конденсатора

I_А = U ωC tgδ, (1)

а активная мощность, рассеиваемая в диэлектрике конденсатора, будет соответственно

Р_А = U² ωC tgδ. (2)

Из выражения (2) следует, что при заданных напряжении U, частоте ω, и емкости С активные потери в диэлектрике будут зависеть от tgδ. Осо-бенно большие потери мощности в изоляции имеют место при больших частотах. Для диэлектриков, применяемых в РЭА, допустимые значения tgδ приведены в ГОСТах на высокочастотные диэлектрики. Чем меньше значение tgδ, тем лучшего качества диэлектрик, т.к. в нем меньше потери энергии. Большие активные потери энергии вызывают нагрев диэлектрика и его преждевременное разрушение.

Наименьшими значениями tgδ = 10^-6 ÷ 10^-5 обладают газообразные диэлектрики. У твердых качественных диэлектриков, применяемых в высо-кочастотных узлах РЭА, tgδ = (2 ÷ 5) ·10^-4; у широко применяемых диэ-лектриков tgδ = (2 ÷ 5) ·10^-3.

Электрическая прочность Е_пр – напряженность электрического поля, при которой наступает пробой диэлектрика или полупроводника. Электрическая прочность является очень важной характеристикой, особенно для диэлектриков, работающих под напряжением выше 1000 В.

Электрическую прочность диэлектрика Е_пр (В/м) в однородном элек-трическом поле вычисляют по формуле Е_пр = U_пр /h, где U_пр – напряжение, при котором произошел пробой диэлектрика, В; h – толщина образца диэлектрика в месте пробоя, м.

Дата добавления: 2014-01-20