
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальный (Гаусовский) закон распределения НСВ
|
|
|
|
Для нормального закона – плотность распределения  имеет вид:
имеет вид:
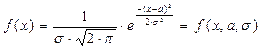 ,
,
где  и
и 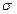 - параметры распределения.
- параметры распределения.
Для данного закона выполняются свойства плотности распределения, а именно:
1)  ;
;
2) 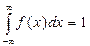 .
.
Можно так же показать, что:
3)  - симметрична относительно прямой
- симметрична относительно прямой 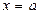 ;
;
4)  , при
, при 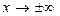 ;
;
5)  имеет максимум в точке
имеет максимум в точке 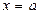 ;
;
6) 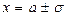 - абсциссы точек перегиба.
- абсциссы точек перегиба.
7) Эти свойства определяют вид графика плотности распределения нормального закона:

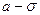
Числовые характеристики нормального закона
1) Можно показать, что математическое ожидание есть:
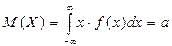 .
.
2) В силу вида графика плотности распределения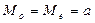 (медиана и мода равны
(медиана и мода равны  ).
).
3) Можно показать, что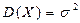 .
.
4) 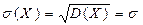 .
.
5) 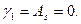
6) 
Отсюда следует, что параметрами нормального закона являются  - математическое ожидание и
- математическое ожидание и 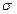 - среднее квадратическое отклонение НСВ. Если параметры
- среднее квадратическое отклонение НСВ. Если параметры 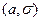 заданы, то закон нормального распределения определен полностью.
заданы, то закон нормального распределения определен полностью.
Рассмотрим влияние изменения параметров  и
и 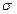 на закон распределения.
на закон распределения.
- При изменении параметра
 график плотности распределения
график плотности распределения  не изменится, а только сдвинется по оси
не изменится, а только сдвинется по оси 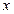 .
.

 При изменении параметра
При изменении параметра 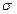 - расстояние между точкой максимума и точкой перегиба меняется, т.е. меняется «широта» графика.
- расстояние между точкой максимума и точкой перегиба меняется, т.е. меняется «широта» графика.
 , т.е. при уменьшении
, т.е. при уменьшении 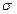 график вытягивается вверх.
график вытягивается вверх.
Для определения функции распределения 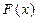 для нормального закона необходимо вычислить интеграл:
для нормального закона необходимо вычислить интеграл:
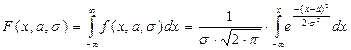 .
.
Этот интеграл в элементарных функциях не выражается. Существуют специальные таблицы функции распределения нормального закона при фиксированных значениях 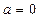 и
и  , т.е. для функции распределения следующего вида:
, т.е. для функции распределения следующего вида:
 ,
,
называемой нормированной функцией Лапласа.
Сама случайная величина 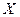 при
при 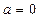 и
и  называется также нормированной. Ее функцию распределения обозначают буквой
называется также нормированной. Ее функцию распределения обозначают буквой 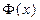 , а соответствующую плотность распределения -
, а соответствующую плотность распределения -  . Для функции
. Для функции 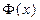 имеются таблицы нормального распределения, при этом можно показать, что
имеются таблицы нормального распределения, при этом можно показать, что - нечетная функция.
- нечетная функция.
Если случайная величина 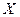 определяется для других значений
определяется для других значений  и
и 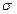 (
( и
и  ), то для того чтобы воспользоваться таблицами
), то для того чтобы воспользоваться таблицами 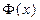 при вычислении
при вычислении 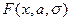 нужно сделать замену переменных
нужно сделать замену переменных 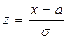 , тогда:
, тогда:
 .
.
Если решается задача нахождения вероятности того, что нормально распределенная НСВ заключена в заданном промежутке 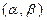 , то:
, то:
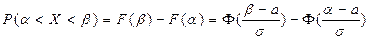 .
.
Если требуется найти вероятность того, что отклонение нормально распределенной величины от параметра  не превосходит по модулю некоторого числа
не превосходит по модулю некоторого числа 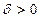 , то тогда очевидно, что:
, то тогда очевидно, что:
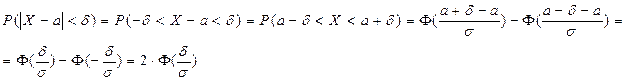 Обычно
Обычно  выражают в долях
выражают в долях 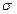 , т.е.
, т.е.  , тогда:
, тогда: 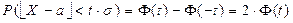 .
.
В частности по таблицам можно посчитать: 
Это означает, что на интервал  приходится соответственно 68,3%; 95,4% и 99,7% от всей площади, расположенной между кривой распределения и осью абсцисс.
приходится соответственно 68,3%; 95,4% и 99,7% от всей площади, расположенной между кривой распределения и осью абсцисс.

Другими словами, лишь в 0,27% наблюдений случайная величина 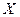 отклоняется от
отклоняется от  более чем на
более чем на  .
.
Такие события можно считать практически невозможными. Поэтому для нормального закона используется «правило трех сигм»: практически достоверно, что случайная величина, подчиненная нормальному закону распределения, отклонится от  не более чем на
не более чем на 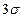 .
.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 899; Нарушение авторских прав?; Мы поможем в написании вашей работы!