Генеральная и выборочная совокупность

Генеральная совокупность - это множество всех объектов (СВ), подлежащих изучению.

Пример: Вклады в банк - генеральная совокупность.

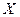- СВ - вклад выбранного вклада.

Выборочная совокупность (или просто выборка) называют множество объектов отобранных для анализа из генеральной совокупности.

Объемом совокупности называют число объектов этой совокупности.

Тогда задача статистики: исследовать СВ 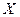по выборочной совокупности, а судить об этой СВ как о СВ принадлежащей генеральной совокупности.

Выборочная совокупность называется репрезентативной если она отражает интересующие нас свойства генеральной совокупности.

Существует три способа представления выборочной совокупности.

1. Простая статическая совокупность.

Если 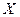- СВ, принимающая значения 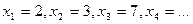, то простая статическая совокупность это прямое перечисление наблюдаемых значений .

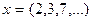Все статические исследования начинаются со сбора данных и построения простой статической совокупности. Дале эти данные преобразуются к одному из двух следующих представлений статистических данных.

2. Вариационный ряд.

В таком виде представляются статические исследования дискретных СВ.

Пусть заданы значения СВ 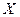: 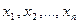, причем 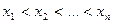- «варианты» выборки с объемом 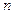, тогда можно построить таблицу:

			…
			…

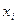
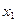
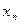
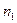
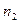
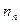
где - частоты «вариантов» 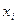(т.е. количество наблюдений, в которых СВ 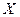принимает значения ).

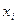Очевидно, что 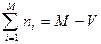выборки.

Эта таблица может содержать и отрицательные частоты , тогда полузаем таблицу закона распределения:

			…
			…

.

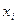
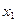
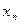
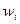
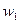
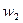
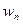
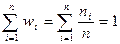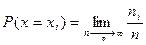(стремление по вероятности).

С ростом объема выборки относительные частоты будут стремиться к соответствующей вероятности.

3. Интегральный вариационный ряд.

В таком виде представляют данные наблюдений непрерывных СВ.

Пример: имеется 25 кроликов с весом, который может быть распределен по следующим интервалам:

Вес	(3-3,5)	(3,5-4)	(4-4,5)	(4,5-5)	(5-5,5)	(5,5-6)	(6-6,5)
Частота

Тогда в общем случае можно построить таблицу для СВ 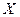в виде интегрального ряда с длинной интервала: :

			…
			…
			…
			…
			…

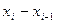
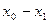
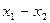
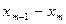
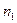
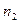
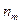
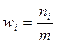
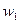
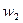
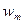
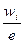
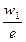
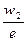
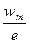
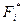
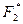
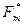
Т.е. СВ 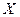принимает значения, попадающие в один из интервалов. В таблице 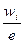- плотность относительных частот, т.е. значение статической плотности распределения, 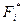- накопленные плотности распределения: .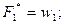

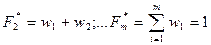Графическая зависимость плотности относительной частоты 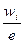от значения 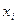СВ имеет вид:

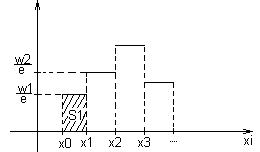
Этот график называется гистограммой относительной частоты. Очевидно, что 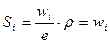, т.к. 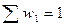, то площадь гистограммы .

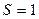Гистограмма это статический аналог плотности распределения СВ.

Дата добавления: 2014-01-20