ДОПИСАТЬ!!!!!! Метод множителей Лагранжа

Для определения себестоимости изделий

Применение дробно-линейного программирования

Пример 6. Для производства двух видов изделий А и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице.

Оборудование I и III типов предприятие может использовать не более 26 и 39 ч соответственно, оборудование II типа целесообразно использовать не менее 4 ч.

Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.

Тип оборудования	Затраты времени на обработку одного изделия, ч
А	В
I II III Затраты на производство Одного изделия, тыс. р.

Дана задача нелинейного программирования

при ограничениях:

Предположим, что функции и непрерывны вместе со своими частными производными.

Для решения задачи составляется функция Лагранжа

где - множители Лагранжа.

Затем определяются частные производные:

Приравняв к нулю частные производные, получим систему

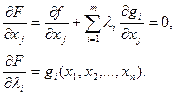
Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным условным экстремумом целевой функции.

Пример 8. Найти точку условного экстремума целевой функции

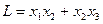
При ограничениях:

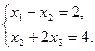
Решение. Составим функцию Лагранжа

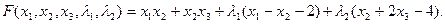
Найдя частные производные и приравняв их к нулю, решим систему

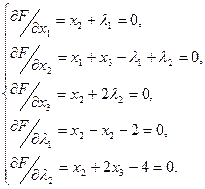
Откуда

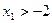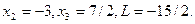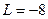Определим характер экстремума, изменяя значения переменных. Изменённые значения должны удовлетворять заданной системе ограничений. Возьмём , например , тогда из системы ограничений получим Возьмём , например , тогда получим Следовательно, - минимальное значение функции.

Ответ. Точка экстремума , при этом минимальное значение функции .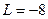

Расчёт экономико-математической модели при

нелинейных реализациях продукции

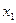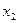Пример 9. Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже кг муки через магазин расходы на реализацию составляют ден. ед., а при продаже кг муки посредством торговых агентов - ден. ед.

Определить, сколько килограммов муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки выделяется для продажи 5000 кг муки.

Дата добавления: 2014-01-11