Принятие решения о замене оборудования в условиях неопределённости и риска

Фирма может принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.

Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.

Полная замена оборудования экономически оправданна при высоком уровне спросе. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.

В данном случае процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно его частичной замены и ремонта.

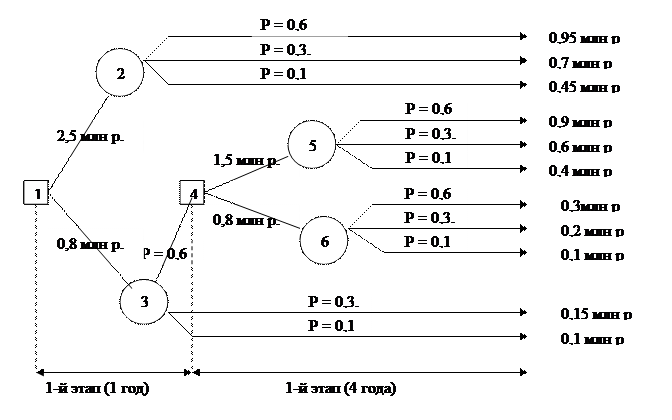
Пример. Рассмотрим задачу о замене оборудования фирмы, представив её в виде «дерева» решений.

Предполагается, что спрос может оказаться высоким, средним и низким.

Дерево имеет два типа вершин: «решающие» и «случайные».

Начиная с «решающей» вершины 1 необходимо принять решение о полной замене оборудования или его ремонте.

Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 «случайные».

Пусть фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют 0,6, 0,3 и 0,1 соответственно. Замена новым оборудованием того же вида, что и старое, обойдётся в 2,5 млн. р., а ремонт старого – в 0,8 млн. р.

Затраты на частичную замену оборудования на более совершенное, чем старое, оцениваются в 1,5 млн. р., а повторный ремонт старого – 0,8 млн. р.

Ежегодные доходы для каждой стратегии фирмы следующие.

1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт,95; 0,7 и 0,45 млн. р. соответственно.

2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается в 0,3; 0,15 и 0,1 млн. р. Соответственно.

3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит 0,9; 0,6 и 0,4 млн. р. соответственно.

4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагается 0,3; 0,2 и 0,1 млн. р. соответственно.

Определить оптимальную стратегию фирмы в замене оборудования.

РЕШЕНИЕ. Оценим результаты каждой стратегии и определим, какие ешения следует принимать в «решающих» вершинах 1 и 4.

Вычисления начнём с 2 этапа. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:

млн. р.,

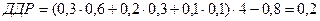млн. р.,

где ДЧЗ – доход от частичной замены оборудования на более совершенное, ДДР – доход от замены оборудования, прошедшего дважды ремонт. Так как ДЧЗ > ДДР, то в вершине 4 выгоднее произвести частичную замену оборудования на более совершенное, при этом доход составит 1,54 млн. р.

Для дальнейших расч1тов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн. р. За 4 года.

Вычислим доходы на 1-м этапе для «решающей» вершины 1:

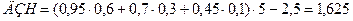млн. р.,

млн. р.,

где ДЗН – доход от замены старого оборудования на новое того же вида, ДЗО – доход от отремонтированного оборудования и дальнейшей замены на более совершенное. Так как ДЗН > ДЗО, то оптимальным решение в вершине 1 является полная замена старого оборудования на новое того же вида.

Элементы системы массового обслуживания (СМО)

1. Формулировка задачи и характеристики СМО

Ожидание является следствием вероятностного характера возникновения потребностей в обслуживании и разброса показателей обслуживающих систем, которые называют системами массового обслуживания (СМО).

Основными элементами СМО являются источники заявок, их входящий поток, каналы обслуживания и выходящий поток.

Входящий поток: на практике наиболее распространённым является простейший поток заявок, обладающий свойствами стационарности, ординарности и отсутствия последействия.

Стационарность характеризуется тем, что вероятность поступления определённого количества требований в течение некоторого промежутка времени зависит только от длины этого промежутка.

Ординарность потока определяется невозможностью одновременного появления двух или более заявок.

Отсутствие последействия характеризуется тем, что поступление заявки не зависит от того, когда и сколько заявок поступило до этого момента.

В этом случае вероятность того, что число заявок, поступивших на обслуживание за промежуток времени t, равно k, определяется по закону Пуассона

,

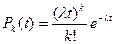где - интенсивность потока заявок, т. е. среднее число заявок в единицу времени:

(чел./мин, р./ч, автом./дн., квт/ч),

где 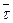- среднее значение интервала времени между двумя соседними заявками.

Случайное время ожидания в очереди начала обслуживания находится по формуле:

,

где 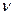- интенсивность движения очереди, т. е. среднее число заявок, приходящих на обслуживание в единицу времени:

,

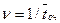где 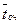- среднее значение времени ожидания в очереди.

Выходящий поток заявок связан с потоком обслуживания в канале, где длительность обслуживания 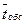является случайной величиной и вычисляется по формуле

,

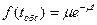где - интенсивность потока обслуживания, т. е. среднее число заявок, обслуживаемых в единицу времени:

(чел./мин, р./дн., кг/ч, докум./дн.),

где 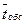- среднее время обслуживания.

Важной характеристикой СМО, объединяющей и , является интенсивность нагрузки

.

2. СМО с отказами

Пример 1. В ОТК цеха работают три контролёра. Если деталь поступает в ОТК, когда все контролёры заняты обслуживанием ранее поступивших деталей, то она проходит непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает один контролёр на обслуживание одной детали, равно 5 мин. Определить вероятность того, что деталь пройдёт ОТК необслуженной, насколько загружены контролёры и сколько их необходимо поставить, чтобы .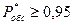

РЕШЕНИЕ. 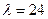дет./ ч = 0,4 дет./ мин, 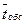= 5 мин, тогда

1. Вероятность простоя каналов обслуживания:

,

где 0! = 1.

2. Вероятность отказа в обслуживании:

3. Вероятность обслуживания:

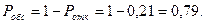
4. Среднее число занятых обслуживанием каналов:

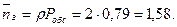
5. Доля каналов, занятых обслуживанием:

6. Абсолютная пропускная способность:

При п = 3 Произведя аналогичные расчёты для п = 4, получим

Так как то произведя расчёты для п = 5, получим

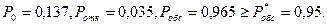
Ответ. Вероятность того, что при п = 3 деталь пройдёт ОТК необслуженной, составляет 21%, и контролёры будут заняты обслуживанием на 53%.

Чтобы обеспечить вероятность обслуживания более 95%, необходимо не менее пяти контролёров.

3. СМО с неограниченным ожиданием

Пример 2. Сберкасса имеет трёх контролёров-кассиров (п = 3) для обслуживания вкладчиков. Поток вкладчиков поступает в сберкассу с интенсивностью 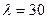чел./ч. Средняя продолжительность обслуживания контролёром-кассиром одного вкладчика мин.

Определить характеристика сберкассы как объекта СМО.

РЕШЕНИЕ. Интенсивность потока обслуживания , интенсивность нагрузки

1. Вероятность простоя контролёров-кассиров в течение рабочего дня:

2. Вероятность застать всех контролёров-кассиров занятыми:

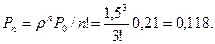
3. Вероятность очереди:

4. Среднее число заявок в очереди:

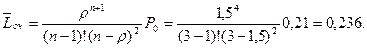
5. Среднее время ожидания заявки в очереди:

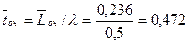мин.

6. Среднее время пребывания заявки в СМО:

мин.

7. Среднее число свободных каналов:

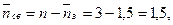
где

8. Коэффициент занятости каналов обслуживания:

9. Среднее число посетителей в сберкассе:

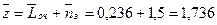чел.

Ответ. Вероятность простоя контролёров-кассиров равна 21% рабочего времени, вероятность посетителю оказаться в очереди составляет 11,8%, среднее число посетителей в очереди 0,236 чел., среднее время ожидания посетителями обслуживания 0,472 мин.

4. СМО с ожиданием и с ограниченной длиной очереди

Пример 3. Магазин получает ранние овощи из пригородных теплиц. Автомобили с грузом прибывают в разное время с интенсивностью 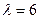машин в день. Подсобные помещения и оборудование для подготовки овощей к продаже позволяют обрабатывать и хранить товар, привезённый двумя автомашинами (т = 2). В магазине работают три фасовщика (п = 3), каждый из которых в среднем может обрабатывать товар с одной машины в течение ч. Продолжительность рабочего дня при сменной работе составляет 12 ч.

Определить, какова должна быть ёмкость подсобных помещений, чтобы вероятность полной обработки товаров была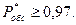

РЕШЕНИЕ. Определим интенсивность загрузки фасовщиков:

авт./дн.

1. Найдём вероятность простоя фасовщиков при отсутствии машин (заявок):

причём 0! = 1,0.

2. Вероятность отказа в обслуживании: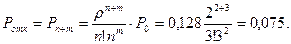

3. Вероятность обслуживания: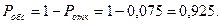

Так как 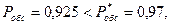произведём аналогичные вычисления для т = 3, получим

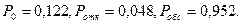
Так как примем т = 4.

Получим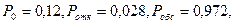

0,972 > 0,97, ёмкость подсобных помещений необходимо увеличить до т = 4.

Для достижения заданной вероятности обслуживания можно увеличить число фасовщиков, проводя последовательно вычисления СМО для п = 4, 5 и т. д. Задачу можно решить, увеличивая ёмкость подсобных помещений, число фасовщиков, уменьшая время обработки товаров.

Найдём остальные параметры СМО для рассчитанного случая при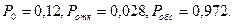

4. Абсолютная пропускная способность:авт./дн.

5. Среднее число занятых обслуживанием каналов (фасовщиков):

6. Среднее число заявок в очереди:

7. Среднее время ожидания обслуживания:

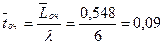дн.

8. Среднее число машин в магазине:

авт.

9. Среднее время пребывания машины в магазине:

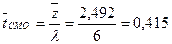дн.

Ответ. Ёмкость подсобных помещений магазина должна вмещать товар, привезённый 4 автомашинами (т = 4), при этом вероятность полной обработки товара будет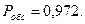

Дата добавления: 2014-01-11