Различные виды агрегатных индексов

Формулы для расчета параметров уравнения квадратического тренда

Таблица 7

Виды индексов	Формулы расчета
Индексы цен	Индексы физических объемов продукции
1. Индекс Ласпейреса
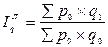
2. Индекс Пааше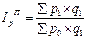
3. Индекс Фишера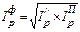

Индексный метод чаще всего применяют в статистике для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. Эти задачи решаются с помощью системы взаимосвязанных индексов переменного состава, постоянного состава и структурных сдвигов.

Индекс переменного состава представляет собой соотношение средних величин какого-либо признака в отчетном и базисном периодах:

I _{пер.сост.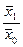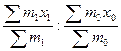} = = (1)

Как видно из формулы (1), индекс переменного состава характеризует изменение среднего уровня признака за счет влияния двух факторов:

1) изменения индивидуальных значений признака x у отдельных единиц статистической совокупности;

2) структурных изменений, то есть изменений доли статистических единиц с одинаковым значением признака x в общей их численности.

Индекс постоянного (фиксированного) состава отражает изолированное влияние первого фактора, т.е. показывает средний размер изменения изучаемого признака x у отдельных статистических единиц и рассчитывается как отношение средних взвешенных величин постоянного состава, т.е. с одними и теми же удельными весами:

I _{пост.сост.} = (2)

Формула (2) легко преобразуется в агрегатную форму обобщающего индекса (так как знаменатель каждой дроби сокращается):

I _{пост.сост.} = (3)

Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака и рассчитывается по формуле:

I _{стр.сдв.} = (4)

В формуле (4) в отличие от формул (2) и (3), наоборот, изменяются только удельные веса отдельных значений признака в предположении, что сами значения сохраняются на прежнем (базисном) уровне.

Индексы переменного и постоянного состава, а также структурных сдвигов увязываются в следующую систему:

I _{пер.сост. =} I _{пост.сост ×} I _{стр.сдв.} (5)

Если в индексах средних величин в качестве удельных весов используются не частоты (число статистических единиц с одинаковыми значениями признака), а частости (т.е. доли одинаковых значений признака в общем объеме статистической совокупности di = 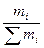), тогда система индексов может быть записана в следующем виде:

I _{пер.сост.} = ;

I _{пост..сост.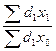} = ; (6)

I _{стр.сдв.} =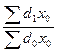

Система индексов переменного, постоянного состава и структурных сдвигов используется для изучения влияния качественных и количественных факторов на динамику среднего уровня цен, себестоимости продукции, фондоотдачи, рентабельности, производительности труда, заработной платы и других важнейших экономических показателей.

Дата добавления: 2014-01-20