Оценка адекватности и точности моделей

Проверка адекватности выбранных моделей реальному процессу строится на анализе случайной компоненты. Принято считать, что модель тренда адекватна описываемому процессу, если значения остаточной компоненты e_t (e_t = y_t-- 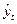) удовлетворяют свойствам случайности, независимости, нормальности распределения. Случайность распределения остаточной компоненты проверяется при помощи критериев серий.

Для проверки независимости используется критерий Дарбина – Уотсона. Для этого рассчитывается фактическое значение критерия по формуле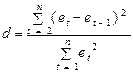

При сравнении расчетной величины d с границами критерия возможны следующие варианты:

1) если d < d_нижн, то гипотеза о независимости случайных отклонений отвергается; (т.е. в ряду остатков есть автокорреляция);

2) если d > d_верх, то гипотеза о независимости случайных отклонений не отвергается;

3) если d_н < d < d_в, то нет достаточных оснований для принятия решений по данному критерию.

Эти варианты относятся к случаю, когда в остатках предполагается наличие положительной автокорреляции, т.е. когда d <2. Когда же расчетное значение d превышает 2, то предполагают наличие в ряду остатков отрицательной автокорреляции. С критическими значениями сравнивается не сам коэффициент d, а 4 – d.

Если случайная компонента удовлетворяет этим свойствам, то выбранную кривую роста можно использовать для определения прогноза.

Для проверки нормальности распределения остаточной компоненты можно использовать показатели асимметрии, эксцесса и их среднеквадратические ошибки. Выборочные характеристики асимметрии и эксцесса и их ошибки по следующим формулам:

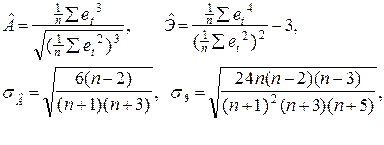
где 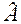- выборочная характеристика асимметрии,

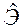- выборочная характеристика эксцесса,

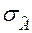-среднеквадратическая ошибка выборочной характеристики асимметрии,

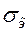- среднеквадратическая ошибка выборочной характеристики эксцесса.

Если одновременно выполняются следующие неравенства:

то гипотеза о нормальном характере распределения случайной компоненты не отвергается. Если же выполняется хотя бы одно из неравенств

то гипотеза о нормальном характере распределения отвергается.

Основными характеристиками качества моделей, выбранных для прогнозирования, являются показатели точности. Понятие точности характеризует степень близости смоделированных (расчетных по определенной модели прогноза) значений (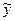) в их совокупности к исходным фактическим данным (y). Чем меньше отличия теоретических значений от эмпирических данных, тем лучше качество модели. Для оценки точности на практике чаще всего используются коэффициент детерминации 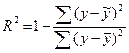, среднеквадратическая ошибка, средняя ошибка аппроксимации .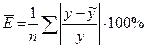

Под верификацией прогноза понимается оценка его достоверности и точности. Ценность прогноза в большей степени определяется его точностью, которая зависит от степени совпадения будущего значения процесса с оценкой этого значения, сделанной заранее. О точности прогноза принято судить по величине погрешности (ошибке) прогноза - разности между прогнозируемым и фактическим значениями исследуемого признака (абсолютная ошибка). Также широко используется и относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя. Очевидно, что оценка прогноза возможна только в случаях:

1) когда период упреждения закончился и исследователь имеет фактические значения прогнозируемого показателя;

2) при разработке ретроспективного прогноза.

При ретроспективном (ex post) прогнозировании исходные данные временного ряда делятся на две части, так чтобы во второй части находились более поздние данные, составляющие обычно примерно 15 % всей информации. Данные первой части используются для построения модели прогноза, а данные второй – для оценки точности построенной модели. При ретроспективном прогнозировании следует иметь в виду, что величину ошибки прогноза нельзя рассматривать как доказательство пригодности или непригодности применяемой модели прогнозирования, так как она получена при использовании лишь части имеющихся данных.

Дата добавления: 2014-01-20