Общие положения химической термодинамики и их использование для определения направления и полноты протекания металлургических реакций

1.1 Закон действия масс и константа равновесия химической реакции

Рассмотрим протекание химической реакции, которая в общем виде может быть описана уравнением

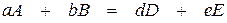, (1.1)

где A, B, D и E – взаимодействующие вещества;

a, b, d и e – стехиометрические коэффициенты в уравнении реакции.

При условии, что параметры состояния системы (давление, температура, объем и др.) остаются постоянными, спустя некоторое время после начала взаимодействия в системе устанавливаются неизменные во времени концентрации продуктов реакции и исходных веществ. Это позволяет говорить о достижении системой состояния термодинамического равновесия, при котором скорости прямой и обратной реакций становятся равными.

Отвлекаясь от сложной природы химического взаимодействия, будем считать, что для протекания реакции достаточно, чтобы в какой-то момент времени частицы взаимодействующих веществ в необходимых количествах оказались в одной точке пространства. Вероятность появления в необходимой точке пространства молекулы одного из реагентов пропорциональна его концентрации. Вероятность одновременного столкновения различных частиц в количестве, отвечающем стехиометрии реакции, равна произведению вероятностей появления в месте столкновения одной или нескольких частиц каждого из реагирующих компонентов. Так как последние пропорциональны концентрациям реагентов, скорость химической реакции оказывается прямо пропорциональной произведению концентраций взаимодействующих веществ, возведенных в степени, равные стехиометрическим коэффициентам в уравнении реакции, то есть

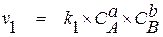, (1.2)

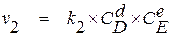, (1.3)

где v1 и v2 – скорости прямой и обратной реакций;

CA, CB, CD и CE – концентрации взаимодействующих веществ;

k1 и k2 – константы скорости прямой и обратной реакций.

Когда реакция достигает состояния равновесия

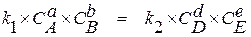, (1.4)

откуда

. (1.5)

При неизменной температуре константы скорости реакций являются постоянными величинами, а их отношение также является постоянной величиной, получившей название константы равновесия химической реакции (К).

Уравнение (1.5) является математической записью закона действия масс, который может быть сформулирован следующим образом: в условиях равновесия химической реакции при постоянной температуре отношение произведения концентраций продуктов реакции, возведенных в степени, равные стехиометрическим коэффициентам в ее уравнении, к произведению концентраций исходных веществ, возведенных в соответствующие степени, является постоянной величиной.

Если в реакции принимают участие вещества, которые находятся в газообразном состоянии, концентрации последних заменяют их парциальными давлениями

, (1.6)

где (%i) – концентрация газообразного вещества, % объемный;

Робщ – давление в системе.

1.2 Законы распределения

В общем случае закон распределения вещества между взаимодействующими фазами может быть сформулирован следующим образом: в условиях равновесия двух соприкасающихся, несмешивающихся фаз при неизменной температуре отношение концентрации вещества в одной из фаз к концентрации его в другой фазе является величиной постоянной. Эта зависимость является частным случаем закона действия масс, так как коэффициент распределения вещества между взаимодействующими фазами можно рассматривать как константу равновесия реакции, в результате которой вещество переходит из одной фазы в другую.

Приведенная выше формулировка закона распределения была получена в результате обобщения ряда экспериментально установленных частных зависимостей. К их числу относятся:

1. Закон Нернста описывает закономерности распределения вещества между конденсированными (жидкими или твердыми) фазами. Согласно этому закону в условиях равновесия двух соприкасающихся, конденсированных фаз при неизменной температуре отношение концентрации вещества в одной из фаз к концентрации его в другой фазе является величиной постоянной.

Математическим выражением закона Нернста является уравнение

, (1.7)

где и 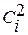– концентрации вещества i в каждой из фаз;

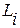– коэффициент распределения вещества i между взаимо-
действующими фазами.

2. Закон Генри описывает закономерности распределения вещества между газообразной и конденсированной фазами. Согласно этой зависимости в условиях равновесия газа с разбавленным раствором вещества в конденсированной фазе концентрация растворенного вещества пропорциональна величине его парциального давления в газовой фазе над раствором.

Математическим выражением закона Генри является уравнение

, (1.8)

где ki – константа Генри;

Pi – парциальное давление вещества в газовой фазе.

Частным случаем закона Генри является закон Сивертса, который учитывает диссоциацию двухатомных молекул газа на отдельные атомы, предшествующую растворению его в конденсированной фазе. Эта зависимость выполняется, например, при растворении в железе кислорода, водорода и азота. Согласно закону Сивертса при равновесии газа с разбавленным раствором его в конденсированной фазе концентрация растворенного газа пропорциональна квадратному корню из величины его парциального давления над раствором.

Покажем справедливость этой зависимости на примере растворения в металле двухатомной молекулы водорода. Процессу растворения предшествует диссоциация молекулы на отдельные атомы, которая может быть описана уравнением

, (1.9)

для которого

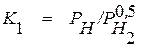. (1.10)

Растворение атомарного водорода в металле может быть описано уравнением реакции

, (1.11)

для которого

. (1.12)

Подставив в уравнение (1.12) величину парциального давления атомарного водорода из уравнения (1.10), получим

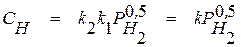. (1.13)

3. Закон Рауля также описывает закономерности распределения вещества между газообразной и конденсированной фазами. Согласно этой зависимости в условиях равновесия газообразной и конденсированной фаз при постоянной температуре давление насыщенного пара растворителя пропорционально мольной доле его в растворе, то есть

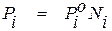, (1.14)

где – давление насыщенного пара чистого растворителя;

Ni – мольная доля растворителя в растворе.

1.3 Термодинамическая активность компонента в растворе

Описанные выше закон действия масс и законы распределения выполняются лишь в ограниченном числе растворов и газовых смесях при относительно невысоких давлениях. Для большинства растворов наблюдаются отклонения от этих зависимостей, причиной которых является наличие взаимодействия между частицами растворителя и растворенного вещества.

Рассматривая характер влияния этого взаимодействия на свойства раствора, в качестве характеристики состояния растворенного вещества будем пользоваться давлением его насыщенного пара (равновесного парциального давления вещества над конденсированной фазой), величина которого характеризует стремление вещества к выходу изданной фазы или химическому взаимодействию.

Рассмотрим раствор двух компонентов. Один из них состоит из молекул вещества А, между которыми действуют силы FA-A, удерживающие его в конденсированном состоянии. Вторым компонентом раствора является вещество В, которое удерживается в конденсированном состоянии силами межчастичного взаимодействия FB-B. Если смешать эти вещества, свойства раствора будут определяться соотношением между силами взаимодействия разнородных частиц FA-B и однородных. При этом возможны следующие случаи.

Возможет случай, когда FA-A = FB-B = FA-B, то есть силы взаимодействия между однородными и разнородными частицами одинаковы. Такое соотношение между силами межчастичного взаимодействия наблюдается при образовании раствора из веществ, обладающих весьма близкими физическими и химическими свойствами. Такие растворы принято называть идеальными или совершенными. Примером их могут служить растворы марганца, никеля и кобальта в железе, свойства которых приближаются к свойствам идеального раствора. Образование этих растворов протекает без тепловых эффектов и изменений объема фаз.

Для идеальных растворов связь между химическим потенциалом вещества и химическим составом раствора описывается зависимостью

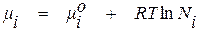, (1.15)

где – химический потенциал компонента i, мольная концентрация
которого в идеальном растворе равняется Ni;

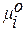– химический потенциал вещества i в стандартном состоянии.

Из уравнения (1.15) видно, что величина химического потенциала вещества в идеальном растворе при заданных значениях температуры и давления однозначно определяется его концентрацией и не зависит от количества и природы других компонентов раствора.

В идеальных растворах выполняется закон Рауля, согласно которому давление насыщенного пара вещества при постоянной температуре пропорционально мольной концентрации его в растворе. Графически эта зависимость отображается прямой, проходящей через начало координат при Ni = 0 и точку при Ni = 1 (рисунок 1.1, линия 1).

В реальных растворах, как правило, наблюдаются отклонения от свойств идеального раствора. Например, их образование обычно сопровождается тепловым эффектом и изменением объема. Это объясняется различием сил взаимодействия между однородными и разнородными частицами, приводящим к образованию группировок частиц, то есть их упорядочению.

Экспериментально установлено, что давление насыщенного пара компонента над реальным раствором увеличивается не пропорционально его концентрации, а по более сложной зависимости (рисунок 1.1, линии 2 и 3).

Кривая 2 на рисунке относится к случаю, когда FA-B > FA-A (FB-B), то есть силы взаимодействия между разнородными частицами больше, чем между однородными. В этом случае растворенное вещество удерживается в конденсированной фазе сильнее, чем в идеальном растворе, и давление насыщенного пара вещества будет ниже, чем над идеальным раствором такого же состава. Такие отклонения от идеальности (от закона Рауля) принято называть отрицательными. Образование подобных растворов обычно сопровождается выделением тепла.

Если FA-B < FA-A (FB-B), то есть силы взаимодействия между разнородными частицами меньше, чем между однородными, в реальном растворе вещество удерживается слабее, чем в идеальном растворе такого же состава. Поэтому кривая 3, которая отражает зависимость давления насыщенного пара вещества от состава раствора, пройдет выше прямой 1. Такие отклонения от идеальности называют положительными. Образование таких растворов обычно протекает с поглощением тепла, а компоненты раствора часто обладают ограниченной взаимной растворимостью. В таких растворах однородные частицы стремятся обособиться в самостоятельные группировки, что при определенных условиях приводит к расслоению системы на разные фазы.

В зависимости от свойств образующих раствор веществ характер кривых 2 и 3 в широком диапазоне изменения концентраций компонентов раствора может существенно различаться. Однако, во всех случаях вблизи точки, отвечающей чистому растворителю (Ni = 1), выполняется закон Рауля, а в области бесконечно разбавленных растворов (Ni = 0) – закон Генри.

Нетрудно показать, что в реальных растворах соотношения (1.5), (1.7), (1.8) и (1.13) – (1.15) не выполняются. Чтобы сделать возможным использование этих соотношений для описания свойств реальных растворов аналитическую концентрацию вещества в них заменяют формальной термодинамической величиной, численное значение которой зависит от состава раствора. Эту величину называют термодинамической активностью или просто активностью компонента раствора (аi).

Чтобы отвечать сформулированному выше требованию активность компонента раствора должна быть численно равной отношению давления насыщенного пара вещества над рассматриваемым раствором (Pi) к давлению насыщенного пара вещества в стандартном состоянии (Pi(ст))

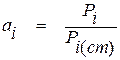. (1.16)

Из уравнения (1.16) можно видеть, что термодинамическая активность компонента раствора является безразмерной величиной. Кроме того, для вещества, взятого в стандартном состоянии, она численно равна единице.

Активность компонента раствора можно также рассматривать как эффективную концентрацию вещества, которая связана с его аналитической концентрацией соотношением

, (1.17)

где 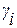– коэффициент активности компонента i, численное значение
которого определяется температурой и составом раствора.

1.4 Стандартные состояния и растворы сравнения при определении
термодинамической активности компонента раствора

Выяснение характера зависимости между термодинамической активностью компонента и составом раствора основано на сопоставлении давления насыщенного пара вещества в реальной системе и так называемых растворах сравнения. В качестве последних берутся растворы, для которых известна количественная зависимость между давлением насыщенного пара вещества и его концентрацией. Обычно в качестве растворов сравнения используют два типа простейших растворов – идеальный и бесконечно разбавленный. Выбор стандартного состояния определяется типом раствора сравнения и наоборот.

На практике чаще других используются следующие сочетания стандартного состояния и раствора сравнения:

1. В качестве стандартного выбирается состояние чистого вещества, то есть 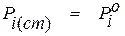при 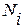= 1. Раствором сравнения в этом случае является идеальный раствор.

При таком выборе стандартного состояния и раствора сравнения коэффициент активности компонента раствора принято обозначать символом , а зависимость между активностью и концентрацией вещества в растворе определяется соотношением (1.17).

2. В качестве стандартного выбирается условное (гипотетическое) состояние вещества, а раствором сравнения служит раствор, обладающий при данной концентрации свойствами бесконечно разбавленного.

В бесконечно разбавленных растворах выполняется закон Генри, в соответствии с которым давление насыщенного пара компонента i вблизи точки 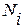= 0, как и в идеальном растворе, пропорционально его концентрации

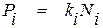. (1.18)

Уравнения (1.17) и (1.18) различаются значениями коэффициентов пропорциональности. В уравнении (1.17) он имеет определенный физический смысл и численно равен реальному давлению насыщенного пара над чистым веществом. В уравнении (1.18) этот коэффициент является чисто эмпирической величиной, найденной опытным путем при очень малых концентрациях вещества в растворе.

В двойных системах численное значение коэффициента ki соответствует тангенсу угла наклона касательной, проведенной к кривым 2 и 3 в точке 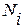= 0. На рисунке 1.1 для раствора с отрицательными отклонениями от идеальности закон Генри отображается при помощи касательной 4, а для раствора с положительными отклонениями от идеальности – касательной 5.

В этом случае стандартным является гипотетическое состояние вещества, при котором оно в чистом виде обладало бы давлением насыщенного пара, численно равным коэффициенту Генри. Его значение можно найти, продолжив касательные 4 и 5 до пересечения с вертикалью, проходящей через точку 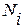= 1.

Если в качестве раствора сравнения выбран раствор, обладающий свойствами бесконечно разбавленного, для обозначения коэффициента активности компонента раствора пользуются символом f. При этом, если в качестве стандартного выбрано гипотетическое состояние вещества, зависимость между активностью и концентрацией компонента в растворе описывается уравнением

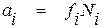. (1.19)

3. Если в диапазоне концентраций от 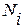= 0 до 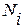= 0,01 (или 1% мас.) кривые 2 и 3 мало отличаются от касательных 4 и 5, в качестве стандартного состояния вещества может быть выбран его однопроцентный раствор. В качестве раствора сравнения в этом случае также используют бесконечно разбавленный раствор. При этом зависимость между активностью и концентрацией компонента в растворе описывается уравнением

, (1.20)

где Ci – концентрация растворенного вещества, % мас.

При определении активности компонента раствора стандартные состояния и растворы сравнения рекомендуется выбирать таким образом, чтобы свойства реального раствора по возможности меньше отличались от свойств раствора сравнения и значения коэффициентов активности компонентов раствора были близки к единице (рисунок 1.2).

В металлургических расчетах активности компонентов часто приходится определять в разбавленных растворах, например, в стали. В этом случае при определении активности растворителя (железа) в качестве стандартного целесообразно выбрать реальное состояние чистого вещества, а в качестве раствора сравнения – идеальный раствор. При определении активности примесей в качестве стандартного состояния целесообразно выбрать однопроцентный раствор вещества в железе, а в качестве раствора сравнения – бесконечно разбавленный раствор.

При определении активности компонента в насыщенных растворах в качестве стандартного целесообразно выбрать реальное состояние чистого вещества. В этом случае активность компонента в насыщенном растворе будет численно равной единице.

1.5 Определение коэффициентов активности компонентов раствора
по методу Вагнера

Для определения термодинамической активности веществ в многокомпонентных растворах обычно пользуются методом Вагнера.

Сущность метода заключается в разложении избыточной термодинамической функции в ряд Тейлора вблизи точки, отвечающей чистому растворителю. Если в качестве стандартного состояния при определении активности компонента раствора принять чистое вещество i, то с учетом соотношения

(1.21)

формулу для определения коэффициента активности компонента раствора можно получить в виде

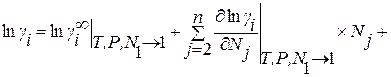
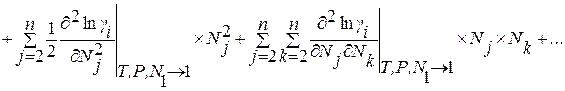, (1.22)

где 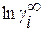– коэффициент активности компонента i в бесконечно
разбавленном двойном растворе.

Входящие в уравнение (1.22) частные производные от логарифма коэффициента активности компонента i по концентрации других компонентов раствора вместе с численными коэффициентами в ряду Тейлора, взятые при постоянных температуре и давлении при бесконечно малых концентрациях растворенных элементов, называют мольными параметрами взаимодействия. Для их обозначения пользуются следующими символами

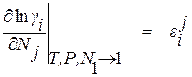, (1.23)

, (1.24)

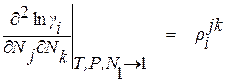. (1.25)

С учетом этих обозначений уравнение (1.22) можно привести к виду

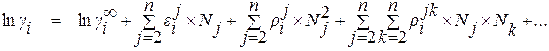. (1.26)

В большинстве случаев необходимая точность вычислений позволяет ограничиться членами ряда нулевой и первой степени. При этом уравнение для расчета коэффициента активности компонента i в многокомпонентном растворе приобретает вид

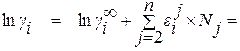
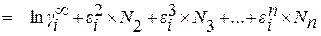. (1.27)

Из уравнения (1.27) видно, что в случае, когда в качестве стандартного состояния выбрано чистое вещество, для расчета коэффициента активности компонента раствора требуются два вида справочных данных – коэффициент активности компонента в бесконечно разбавленном двойном растворе и мольные параметры взаимодействия первого порядка.

Если в качестве стандартного состояния выбран однопроцентный разбавленный раствор компонента i в растворителе, с учетом соотношения

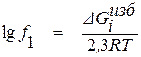(1.28)

формула для определения коэффициента активности компонента раствора будет иметь вид

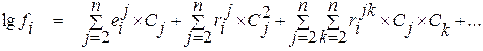, (1.29)

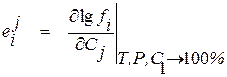, (1.30)

, (1.31)

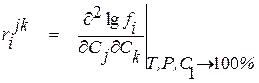. (1.32)

Символы 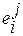, 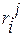и в формулах (1.29) – (1.32) называют массовыми параметрами взаимодействия. Символом 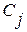в этих уравнениях обозначена концентрация компонентов раствора, выраженная в массовых процентах.

В большинстве случаев коэффициент активности вещества в многокомпонентном растворе с достаточной точностью можно определить при помощи уравнения

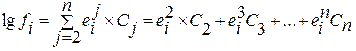. (1.33)

Из уравнения (1.33) видно, что при выборе в качестве стандартного состояния однопроцентного раствора компонента в растворителе, обладающего свойствами бесконечно разбавленного, для расчета коэффициента активности компонента i раствора требуются только лишь значения массовых параметров взаимодействия первого порядка. Свободный член в этом уравнении отсутствует, так как в бесконечно разбавленном растворе 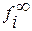= 1 и, следовательно, = 0.

В практических расчетах с использованием параметров взаимодействия могут оказаться полезными следующие формулы

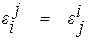, (1.34)

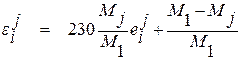, (1.35)

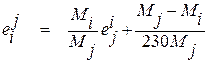. (1.36)

В формулах (1.34) – (1.36) символам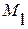и , и 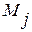обозначены атомные массы растворителя, компонента i и компонента j.

1.6 – Направление реакции при изменении условий ее протекания

При изменении параметров системы изменяется и соотношение между равновесными активностями взаимодействующих веществ. Качественно характер этого изменения можно установить с помощью принципа Ле-Шателье, который может быть сформулирован следующим образом.

Если на систему, находящуюся в состоянии термодинамического равновесия, оказано внешнее воздействие, изменяющее параметры системы, определяющие состояние равновесия, в системе протекают процессы, которые уменьшают эффект произведенного воздействия.

Кислородные конвертеры, мартеновские и дуговые электросталеплавильные печи относятся к открытым сталеплавильным агрегатам, в которых процессы протекают при практически постоянном давлении и изменении температуры в широких пределах. Качественно охарактеризовать влияние температуры на величину константы равновесия химической реакции можно при помощи уравнения изобары Вант-Гоффа

. (1.37)

Из уравнения (1.37) видно, что знак производной от логарифма константы равновесия реакции по температуре совпадает со знаком изменения энтальпии при протекании химической реакции. Это означает, что с ростом температуры константы равновесия экзотермических реакций (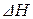< 0) уменьшаются, а константы равновесия эндотермических реакций (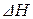> 0) увеличиваются.

При этом абсолютное значение производной от логарифма константы равновесия реакции по температуре прямо пропорционально величине изменения энтальпии при протекании химической реакции. Отсюда следует, что изменение температуры не оказывает сильного влияния на величину констант равновесия реакций, протекающих с малыми тепловыми эффектами. Поэтому, рассматривая протекание этих реакций в ограниченном диапазоне температур, влиянием температуры на величину констант равновесия реакций с достаточной для практических целей точностью можно пренебречь. Для реакций, протекание которых сопровождается большими тепловыми эффектами, учет влияния температуры на величину констант равновесия реакций является обязательным.

1.7 Определение численного значения константы равновесия реакции
по справочным данным

В общем случае связь между значениями изменения энергии Гиббса и константы равновесия химической реакции описывает уравнение

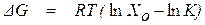, (1.38)

где – выражение подобное константе равновесия реакции, но составленное не из равновесных, а из фактических активностей взаимодействующих веществ.

Согласно второму началу термодинамики произвольное протекание химической реакции возможно в условиях, когда оно сопровождается уменьшением энергии Гиббса системы (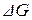< 0). Поэтому, в зависимости от соотношения между значениями величин и 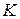, в системе возможны следующие процессы:

1. При высоких активностях исходных взаимодействующих веществ и малых активностях продуктов реакци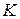и < и 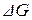< 0. В этих условиях возможно произвольное протекание реакции в направлении образования дополнительного количества продуктов взаимодействия.

2. При высоких активностях продуктов реакции и малых активностях взаимодействующих веществ > 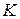и 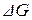> 0. При этом произвольное протекание реакции возможно только в направлении образования дополнительного количества исходных веществ.

3. Если фактические активности взаимодействующих веществ и продуктов реакции соответствуют их равновесным значениям, = 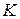и 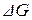= 0. При этом система находится в состоянии термодинамического равновесия.

Если взаимодействующие вещества находятся в стандартных состояниях, = 1 и = 0. При этом соотношение (1.38) приобретает вид

, (1.39)

где 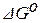– изменение энергии Гиббса реакции образования соединений
из веществ в стандартных состояниях (стандартное значение
изменения энергии Гиббса реакции).

Обычно в справочной литературе приводятся сведения об изменении энтальпии () и изменении энтропии () реакций образования химических соединений из веществ, взятых в стандартном состоянии. Зная эти величины, можно рассчитать стандартное значение изменения энергии Гиббса реакции из уравнения

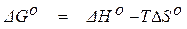. (1.40)

После этого при помощи уравнения (1.39) можно определить численное значение константы равновесия реакции при выбранной температуре.

При этом если нет специальной оговорки, под веществом в стандартном состоянии обычно подразумевается чистое вещество в том агрегатном состоянии, в котором оно устойчиво при выбранной температуре и давлении 0,1 МПа.

Если требуется определить константу равновесия реакции с участием компонентов раствора, найденное согласно уравнению (1.40) значение изменения энергии Гиббса реакции образования соединения из веществ в стандартных состояниях необходимо просуммировать с изменением энергии Гиббса реакций растворения взаимодействующих веществ.

Рисунок 1.1 – Зависимость давления насыщенного пара компонента от концент-
рации вещества в двухкомпонентной системе

Рисунок 1.2 – Иллюстрация к использованию правила выбора стандартного
состояния и раствора сравнения при определении активности
компонента раствора

Дата добавления: 2014-01-20