Цветовые модели пользователя. Модели HSV, HSB

Цветовые модели HSV и HSB (от англ. Нue, Saturation, Value, Brightness - тон, насыщенность, величина, яркость) являются, в отличие от рассмотренных выше моделей, ориентированными на человека и его интуитивные представления о выборе цвета.

Рассмотрим цилиндрические координаты в трехмерном евклидовом пространстве, H - угол в горизонтальной плоскости от оси Ox, S - радиус в горизонтальной плоскости (расстояние до оси Oz), V и B - высота (по оси Oz). Все цветовое пространство представляет из себя, в первом случае - перевернутую шестигранную пирамиду (рис.1.15), во втором случае – шестигранную призму или цилиндр (правильный шестиугольник заменили окружностью). Нижняя точка пирамиды соответствует всему основанию призмы или цилиндра.

	Можно также заметить, что основание пирамиды представляет из себя проекцию RGB-куба вдоль главной диагонали со стороны белого. Вершины основания пирамиды соответствуют чистым основным цветам (красному, желтому, зеленому, голубому, синему и фиолетовому). При их смешивании друг с другом в разных пропорциях точка, соответствующая цвету, перемещается по основанию пирамиды.
Рис. 1.15. Цветовая модель HSV.	Смешивая противополож­ные цвета (например,

желтый и синий), можно получить белый. Добавляя к какому-либо чистому цвету черный, мы будем спускаться по пирамиде, получая различные оттенки, при этом диапазон S будет уменьшаться вплоть до нуля. На оси S = 0 (оттенки серого) значение H не определено.

Алгоритмы преобразования из RGB в HSV и обратно приведены ниже:

{ // H - в градусах

maxVal = maximum(R,G,B); minVal = minimum(R,G,B); V = maxVal;

if(maxVal = = 0) S = 0;

else S = (maxVal - minVal)/maxVal;

if(S = = 0) H = UNDEFINED;

else

{ if(R == maxVal) H = (G-B)/(maxVal - minVal);

else if(G == maxVal) H = 2 + (B-R)/(maxVal - minVal);

else if(B == maxVal) H = 4 + (R-G)/(maxVal - minVal);

H = H * 60;

if(H < 0)

H = H + 360; }

}

Листинг 1.1. Переход от RGB к HSV

{ // H - в градусах

if(S = = 0) { // находимся на оси симметрии - оттенки серого

R = V; G = V; B = V; }

else { // floor(x) возвращает наибольшее целое <= x

sector = floor(H / 60); frac = H / 60 - sector; // дробная часть H/60

T = V * (1 - S); P = V * (1 - S*frac); Q = V * (1 - S*(1 - frac));

switch(sector)

{ case 0: R = V; G = Q; B = T; break;

case 1: R = P; G = V; B = T; break;

case 2: R = T; G = V; B = Q; break;

case 3: R = T; G = P; B = V; break;

case 4: R = Q; G = T; B = V; break;

case 5: R = V; G = T; B = P; break; }

}

}

Листинг 1.2. Переход от HSV к RGB

Есть также и другие цветовые модели пользователя, схожие тем, что все они имеют координаты H и S, например, модели HLS и HIS. Различаются эти модели лишь в несущественных для пользователя деталях (например, параметры в них могут быть по-разному отнормированы или приведены).

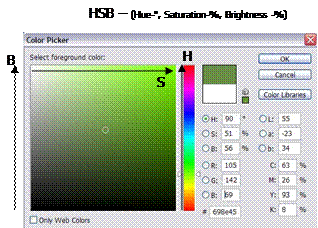
	Системы же компьютерной графики предлагают пользователю инструментарий, в котором цвет не задается числовыми значениями, а выбирается на линейных и плоских шкалах (рис.1.16). Это практически полностью нивелирует для пользователя различия между моделями такого типа. Важно только их наличие и реализация связи с другими моделями.
Рис.1.16.Пример интерфейса по выбору цвета с указанием осей модели HSB

5. Цветовые модели, разделяющие яркость и цвет: Y**

Существует несколько тесно связанных цветовых моделей, которые объединяет то, что в них используется явное разделение информации о яркости и цвете. Компонента Y соответствует одноименной компоненте в модели CIE XYZ и отвечает за яркость. Такие модели находят широкое применение в телевизионных стандартах, так как исторически необходима была совместимость с черно-белыми телевизорами, которые принимали только сигнал, соответствующий Y. Также они применяются в некоторых алгоритмах обработки и сжатия изображений и видео.

Дата добавления: 2014-01-20