Критерий Сильвестра

Теорема (детерминантный критерий Сильвестра)

Квадратичная форма

1) положительна тогда и только тогда, когда ;

2) отрицательна тогда и только тогда, когда ;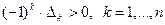

3) неотрицательна тогда и только тогда, когда ;

4) неположительна тогда и только тогда, когда ;

5) знакопеременна – в остальных случаях.

Из данной теоремы следует, что квадратичная фора квазиположительна тогда и только тогда, когда выполняется условие 3, но не выполняется условие 1 (т.е. все главные миноры неотрицательны, но хотя бы один из них равен нулю[1]), и квазиотрицательна тогда и только тогда, когда выполняется условие 4, но не выполняется условие 2.

Для установления знакоопределенности квадратичной формы может быть предложена следующая схема:

1. Составляется матрица квадратичной формы.

2. Определяются знаки ее угловых миноров.

3. Если знаки всех угловых миноров положительны, то квадратичная форма положительна; если некоторые из знаков заменяются нулями ("мягкое" нарушение правила постоянства знаков) – нужно исследовать все главные миноры; если все они неотрицательны, то квадратичная форма квазиположительна (в обоих случаях – неотрицательна);

4. Если знаки угловых миноров чередуются, начиная с минуса, то квадратичная форма отрицательна; если некоторые из знаков заменяются нулями ("мягкое" нарушение правила чередования знаков) – нужно исследовать все главные миноры; если все главные миноры порядка k имеют знак (-1) ^k (или равны нулю), то квадратичная форма квазиотрицательна (в обоих случаях – неположительна);

5. Если ни первое (п.3), ни второе (п.4) правила знаков не соблюдаются ("грубое" нарушение правила постоянства или чередования знаков: "+" заменяется на "-" или наоборот), то квадратичная форма знакопеременна.

Наглядно данное правило представлено в следующей таблице:

Знакоопределенность квадратичной формы				………..
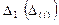
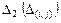
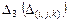
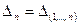
Положительная	+	+	+	……….	+
Отрицательная	–	+	–	……….	(–1) ^n
Неотрицательна	+ или 0	+ или 0	+ или 0	………..	+ или 0
Неположительна	– или 0	+ или 0	– или 0	………..	(–1) ^n или 0
Нулевая				………..

Замечания (следствия из теоремы):

1. Если все угловые миноры положительны, то и все главные миноры положительны;

2. Если знаки угловых миноров чередуются, начиная с "–", то и знаки всех главных миноров данного порядка совпадают со знаком соответствующего углового минора;

3. Если какой-нибудь угловой (главный) минор четного порядка (например, второго) отрицателен, то матрица неопределена (квадратичная форма знакопеременна);

4. Если знаки каких-нибудь угловых (главных) миноров нечетного порядка (например, первого и третьего) противоположны, то матрица неопределена (квадратичная форма знакопеременна);

5. Если какие-нибудь главные миноры одного порядка (например, первого) имеют противоположные знаки, то матрица неопределена (квадратичная форма знакопеременна).

Приведенная выше схема – не догма. В каждом конкретном случае следует искать наискорейший путь к решению проблемы. Например, если Вы видите, что на главной диагонали матрицы стоят элементы различных знаков, то сразу можно сделать вывод относительно неопределенности данной матрицы (главные миноры первого порядка имеют разные знаки), т.е. знакопеременности соответствующей квадратичной формы.

Пример

Исследовать квадратичную форму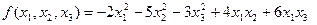

на знакоопределенность.

Дата добавления: 2014-01-20