
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Преобразования Галилея
|
|
|
|
РИС. 2-3
Система K¢ движется со скоростью 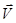 относительно K.
относительно K.
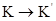
| 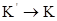
|

| 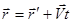
|

| 
|
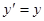
| 
|

| 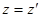
|

| 
|
Равенство  означает абсолютность времени. Это особенность классической механики вообще, когда предполагается, что
означает абсолютность времени. Это особенность классической механики вообще, когда предполагается, что 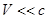 - скорость передачи сигнала бесконечна.
- скорость передачи сигнала бесконечна.
Преобразование скоростей

РИС. 2-4
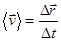 ;
;  .
.
Дифференцируя  по времени, находим закон преобразования скоростей.
по времени, находим закон преобразования скоростей.
 - скорость в неподвижной системе отсчета;
- скорость в неподвижной системе отсчета;
 - скорость в движущейся системе отсчета.
- скорость в движущейся системе отсчета.
Так как  , то
, то 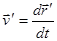 .
.
Подставив  , получаем
, получаем  .
.
Преобразование ускорений


 .
.
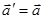 - ускорение инвариантно относительно преобразований Галилея.
- ускорение инвариантно относительно преобразований Галилея.
Показать самостоятельно, что расстояние между двумя точками инвариантно относительно преобразований Галилея: 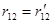
(это легко сделать, если вспомнить, как определяется расстояние между двумя точками в декартовой системе.)
2-ой закон Ньютона и преобразования Галилея
Основной закон динамики (2-ой закон Ньютона) инвариантен относительно преобразований Галилея.
Рассмотрим преобразование второго закона Ньютона 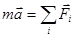 .
.
Ускорение  инвариантно относительно преобразований Галилея.
инвариантно относительно преобразований Галилея.
Стоящая справа сила всегда является функцией инвариантных величин: или расстояний между точками, или разности скоростей взаимодействующих частиц.
Например, упругие силы:
 .
.
В движущейся системе координат 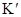 :
: 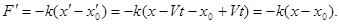
Итак, 2-ой закон Ньютона (основное уравнение динамики) инвариантен относительно преобразований Галилея:  .
.
Уравнения механики Ньютона инвариантны относительно преобразований Галилея - принцип относительности Галилея.
Обобщение: законы природы одинаковы (инвариантны) во всех ИСО.
Точнее (по Эйнштейну):
законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из ИСО относятся эти изменения.
Сказанное справедливо при любых скоростях относительного движения, однако при  (строго говоря, вместо знака равно нужно использовать знак приблизительно!) нужно применять уже не преобразования Галилея, а преобразования Лоренца.
(строго говоря, вместо знака равно нужно использовать знак приблизительно!) нужно применять уже не преобразования Галилея, а преобразования Лоренца.
 Движение, впрочем, может по-разному выглядеть в различных ИСО:
Движение, впрочем, может по-разному выглядеть в различных ИСО:
РИС. 2-5
Траектория свободно падающей материальной точки  :
:
-прямая вертикальная линия для наблюдателя в вагоне;
-парабола для внешнего наблюдателя.
Покажем продуктивность высказанных соображений; выведем, пользуясь принципом относительности Галилея, уравнение движения тела переменной массы, например ракеты или реактивного снаряда.

РИС. 2-6
Воспользуемся приближением материальной точки.
Формулировка задачи: в момент  материальная точка P имеет массу
материальная точка P имеет массу  ; присоединяемая (отделяемая) масса имеет скорость
; присоединяемая (отделяемая) масса имеет скорость  .
.
Введем инерциальную систему  , скорость которой равна скорости
, скорость которой равна скорости 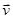 точки
точки  в момент
в момент  , т.е. точка
, т.е. точка  покоится в ИСО
покоится в ИСО  (сопутствующая ИСО).
(сопутствующая ИСО).
За интервал времени 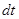 (от
(от  до
до  ) материальная точка
) материальная точка  приобретет импульс
приобретет импульс 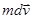 . Этот импульс точка получает, во-первых, за счет действия внешних сил
. Этот импульс точка получает, во-первых, за счет действия внешних сил 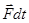 и, во-вторых, за счет присоединения (отделения) массы
и, во-вторых, за счет присоединения (отделения) массы  :
:
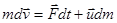 .
.
Поделив на 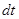 , получаем
, получаем
 - уравнение Мещерского.
- уравнение Мещерского.
Мещерский Иван Всеволодович (1859 -1935 г.г.) – советский ученый в области теоретической и прикладной механики. В 1882 г. окончил физико-математический факультет Санкт-Петербургского университета, с 1890 г. – приват-доцент кафедры механики, с 1902 г. – заведующий кафедрой
Санкт-Петербургского, затем Ленинградского политехнического института. Основополагающие труды по механике тел переменной массы, ставшие основой решения различных проблем реактивной техники, небесной механики. Последовательно проводил в жизнь идею тесной связи теоретической и прикладной механики.
Полученное в одной конкретной инерциальной системе (сопутствующая ИСО), это уравнение - в силу принципа относительности Галилея - справедливо в любой другой ИСО.
Слагаемое  - реактивная сила.
- реактивная сила.
Если  (потеря массы) и
(потеря массы) и  направлена в сторону, противоположную
направлена в сторону, противоположную 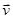 , то
, то 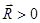 - реактивная сила вызывает ускорение материальной точки.
- реактивная сила вызывает ускорение материальной точки.
Два частных случая
Случай 1 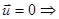
 = 0.
= 0.
Уравнение похоже на основное уравнение динамики, но с массой, зависящей от времени:
 (под
(под 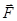 подразумевается равнодействующая всех сил, действующих на материальную точку).
подразумевается равнодействующая всех сил, действующих на материальную точку).
Случай 2  ,
, 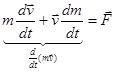




(в этом случае действие силы определяет изменение импульса  тела с переменной массой).
тела с переменной массой).
Закон сохранения массы
Мы говорили о сохранении массы (числа частиц и т.п.), исходя из релятивистской связи между массой и энергией. Обоснуем закон, исходя из принципа относительности Галилея.
Пусть два тела (две материальные точки) с массами  и
и 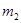 сталкиваются между собой и превращаются в единое тело (материальную точку) с массой
сталкиваются между собой и превращаются в единое тело (материальную точку) с массой  (пластилиновые шары, химическая или ядерная реакция). Спрашивается, какова будет масса составного тела. Покажем, что
(пластилиновые шары, химическая или ядерная реакция). Спрашивается, какова будет масса составного тела. Покажем, что  .
.
Рассматриваем движение тел в некоторой «покоящейся» системе  . Пусть скорости до столкновения -
. Пусть скорости до столкновения -  и
и  , после столкновения скорость составного тела -
, после столкновения скорость составного тела - 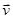 .
.
Из закона сохранения импульса следует: .
.
В системе отсчета 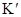 (движущейся со скоростью
(движущейся со скоростью 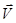 ) скорости соответственно
) скорости соответственно
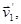
 ,
, 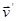 , а закон сохранения импульса справедлив с прежней силой:
, а закон сохранения импульса справедлив с прежней силой:
 .
.
Скорости в системе 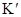 :
:
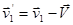 ,
, 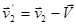 ,
,  .
.
Отсюда
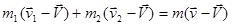 .
.
Принимая во внимание закон сохранения импульса в системе  , получаем:
, получаем:
 - свойство аддитивности массы.
- свойство аддитивности массы.
Если в результате химической реакции из нескольких различных атомов получается несколько иных молекул, то можно обобщить: сумма масс веществ до реакции равна сумме масс веществ после реакции.
Однако это соотношение верно лишь приближенно, так как принцип относительности Галилея является частным случаем принципа относительности Эйнштейна (при 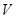 «
«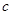 ). Релятивистская теория требует в балансе масс учитывать и энергию.
). Релятивистская теория требует в балансе масс учитывать и энергию.
Для случая химических реакций поправка пренебрежимо мала.
Пример
C + O2 → CO2 + 4∙1012эрг.
12 г 32 г 44г
Дефект массы: 


 г.
г.
Относительная погрешность 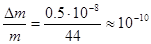 .
.
В случае ядерных реакций (деления или синтеза) энергетический выход значительно больше, так что и дефект массы  - вполне заметная, существенная величина.
- вполне заметная, существенная величина.
Теорема о движении центра масс
Для любой материальной точки  ,
,
иначе  , где
, где 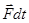 - количество движения.
- количество движения.
Для системы материальных точек количество движения:
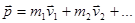 .
.
Введем понятие центра масс системы:
это такая воображаемая точка, радиус-вектор которой  задается через
задается через
радиусы-векторы 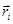 и массы
и массы  всех точек системы следующим образом:
всех точек системы следующим образом:
 , где
, где  - полная масса системы.
- полная масса системы.
Продифференцируем по  и умножим на
и умножим на  :
:
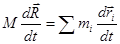 ;
;  - скорость движения центра масс.
- скорость движения центра масс.
 Þ
Þ .
.
Центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила - векторной сумме всех внешних сил, действующих на систему.
Если система материальных точек является замкнутой, то сумма всех внешних сил  .
.
Следовательно, 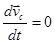 Þ
Þ  .
.
Центр масс замкнутой системы движется равномерно и прямолинейно.
 Понятие о приведенной массе
Понятие о приведенной массе
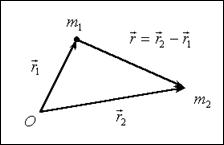
РИС. 2-7
Пусть система состоит из двух материальных точек с массами  m 1 и m 2. Уравнения движения этих двух точек:
m 1 и m 2. Уравнения движения этих двух точек: 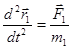 ,
,  .
.
Вычитая из второго уравнения первое, находим:
 .
.
Если система замкнутая, то внешние силы отсутствуют и, в соответствии с 3-им законом Ньютона,  .
.
Учитывая, что 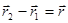 , получаем:
, получаем:
 .
.
Вводя обозначение 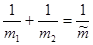 ,
,
получаем уравнение:  , где
, где 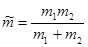 - приведенная масса.
- приведенная масса.
Уравнение описывает движение частиц вокруг общего центра масс.
Если, например,  , то, поделив на
, то, поделив на 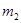 числитель и знаменатель, получаем:
числитель и знаменатель, получаем:
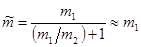 - движение легкой частицы вокруг тяжелой.
- движение легкой частицы вокруг тяжелой.
Приведенная масса – целесообразное обозначение, облегчающее решение ряда задач.
Эффект Мессбауэра (ядерный  - резонанс) как яркий пример законов сохранения
- резонанс) как яркий пример законов сохранения
 (данный материал можно пропустить)
(данный материал можно пропустить)
РИС. 2-8
Испускание (или поглощение)  - кванта с энергией
- кванта с энергией 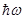 атомным ядром при переходе из состояния
атомным ядром при переходе из состояния 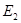 в состояние
в состояние  .
.
Разность внутренних энергий ядра 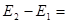 ћw (w - частота); разность импульсов
ћw (w - частота); разность импульсов 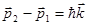 ,
,  - волновой вектор
- волновой вектор  - кванта (
- кванта (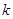 - волновое число).
- волновое число).
Изменение полной энергии ядра:
 ,
,
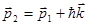 ,
,
 ,
,
 ,
,
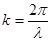 ,
, 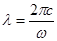 ,
,  Þ
Þ  .
.
Если бы излучающее ядро оставалось неподвижным, то излучаемая частота определялась бы только разностью внутренних энергий в начальном и конечном состояниях  . Однако ядро приобретает так называемую отдачу
. Однако ядро приобретает так называемую отдачу  , причем могут встречаться скорости
, причем могут встречаться скорости 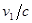 ~10-4.
~10-4.
Итак, излучаемая энергия зависит от скорости излучающего ядра, причем ядра могут получать различные скорости  , значит будут излучаться различные
, значит будут излучаться различные
 - кванты. Спектр будет состоять из набора линий, соответствующих различным скоростям атомов – фактически из широкой полосы, отражающей распределение атомов по скоростям отдачи. Однако, если поместить излучающие ядра (атомы) в кристалл, поставив их в условия, когда они не могли бы передавать энергию колебаниям решетки (для этого нужно, чтобы энергия
- кванты. Спектр будет состоять из набора линий, соответствующих различным скоростям атомов – фактически из широкой полосы, отражающей распределение атомов по скоростям отдачи. Однако, если поместить излучающие ядра (атомы) в кристалл, поставив их в условия, когда они не могли бы передавать энергию колебаниям решетки (для этого нужно, чтобы энергия  - квантов была не слишком велика,
- квантов была не слишком велика,  кэВ, а температура кристалла достаточно низка,
кэВ, а температура кристалла достаточно низка, 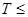 100 K), то в этом случае обмен импульсом будет происходить с кристаллом в целом. При этом уравнение сохранения энергии нужно переписать так:
100 K), то в этом случае обмен импульсом будет происходить с кристаллом в целом. При этом уравнение сохранения энергии нужно переписать так:
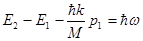 . Здесь
. Здесь  - макроскопическая величина,
- макроскопическая величина, 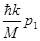 - пренебрежимо малая величина.
- пренебрежимо малая величина.
Получается чрезвычайно узкая линия, ее относительная ширина в первых опытах достигала 10-10, сейчас меньше 10-15, так что с помощью эффекта Мессбауэра удается наблюдать одно из следствий общей теории относительности (ОТО) - влияние гравитационного поля Земли на частоту излучения.
Рудольф Людвиг Мессбауэр (родился 31.01.1929 г. в Мюнхене) – Нобелевская премия 1961 г. «за исследование резонансного поглощения  - излучения и открытие эффекта, названного его именем».
- излучения и открытие эффекта, названного его именем».
Работа и энергия
Работа силы 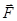 на перемещении
на перемещении 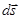 производится проекцией (составляющей) силы на это направление
производится проекцией (составляющей) силы на это направление 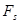 :
:
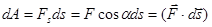 - скалярное произведение.
- скалярное произведение.
В зависимости от направления силы по отношению к перемещению (т.е. от знака проекции 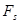 ) знак работы будет разным - положительным, отрицательным, или работа будет равна нулю при
) знак работы будет разным - положительным, отрицательным, или работа будет равна нулю при 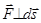 .
.
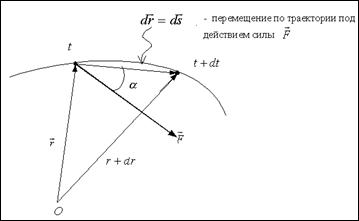
РИС. 2-9
Работа силы 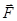 на траектории
на траектории  между точками 1 и 2 равна сумме работ на элементарных отрезках (вся траектория разбивается на участки
между точками 1 и 2 равна сумме работ на элементарных отрезках (вся траектория разбивается на участки 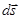 , такие, что они хорошо аппроксимируют криволинейную траекторию отрезками прямых линий):
, такие, что они хорошо аппроксимируют криволинейную траекторию отрезками прямых линий):

РИС. 2-10
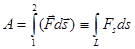
 - криволинейный интеграл вектора
- криволинейный интеграл вектора 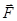
 по траектории
по траектории  .
.

РИС. 2-11
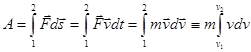 (
( ).
).
На участке 1-2 совершена работа.
Можно записать работу и по-другому:
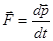 (второй закон Ньютона),
(второй закон Ньютона),  , отсюда
, отсюда
 .
.
Если 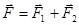 , то
, то 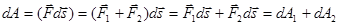 .
.
Для конечных перемещений:
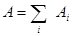 - работа равнодействующей нескольких сил равна сумме работ каждой из этих сил.
- работа равнодействующей нескольких сил равна сумме работ каждой из этих сил.
Размерности:
1 Н × 1м = 1 Дж; 1 дина ×1 см = 1 эрг; 1 Дж = 107 эрг;
1 эВ = 1.602 × 10-12 эрг – энергия, приобретаемая электроном при прохождении разности потенциалов 1 В. 1 кэВ = 103 эВ, 1 МэВ = 106 эВ.
Мощность: 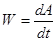 [Дж /с = Вт ];
[Дж /с = Вт ];  .
.
Поскольку работу можно записать в виде 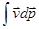 , то в случае массы, не зависящей от скорости, то есть в нерелятивистском приближении,
, то в случае массы, не зависящей от скорости, то есть в нерелятивистском приближении, 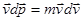 .
.
Поскольку  , при выполнении работы по перемещению точки с массой
, при выполнении работы по перемещению точки с массой  из положения 1 в положение 2 (скорости соответственно
из положения 1 в положение 2 (скорости соответственно  и
и 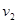 ) имеем:
) имеем:
 .
.
Кинетическая энергия материальной точки:
 .
.
Таким образом,  .
.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1558; Нарушение авторских прав?; Мы поможем в написании вашей работы!