
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Деформативные характеристики бетона
|
|
|
|
Классы и марки бетона
Классы и марки являются показателями качества бетона (по какому-либо признаку) и устанавливаются СНиП 52-01-2003. Различают следующие классы: В – по прочности на сжатие; Вt – по прочности на осевое растяжение.
Классом бетона по прочности на сжатие В называют наименьшее контролируемое значение временного сопротивления сжатию стандартных кубов (с ребром 150 мм, испытанных с соблюдением требований ГОСТ), гарантированное с обеспеченностью 0,95.
По СНиП 52-01-2003 для бетонных и железобетонных конструкций предусмотрены следующие классы тяжелого бетона по прочности на сжатие:
В10; В15; В20; В25; В30; В35; В40; В45; В50; В55; В60.
Число, стоящее после буквы В, соответствует гарантированной прочности на осевое сжатие в МПа, с обеспеченностью 95%.
Рассмотрим подробнее понятие «класс бетона» и как он назначается.
Прочностные характеристики бетона обладают определенной изменчивостью, т.е. являются случайными величинами (с позиций теории вероятностей). Тогда, чтобы обеспечить достаточную надежность конструкции, в расчетах надо принимать наименьшие из возможных значения прочности, соответствующие заданной вероятности (иначе – такие значения прочности, которые в подавляющем большинстве случаев были бы ниже возможных фактических значений прочности в конструкции). Установить такие значения можно с помощью методов теории вероятностей и математической статистики.
По результатам испытаний образцов строят опытные гистограмму и статистическую кривую распределения прочности бетона (рис. 13), характеризующие ее изменчивость. По оси абсцисс откладывают значения прочности R 1, R 2,… Rk, а по оси ординат – числа n 1, n 2, … nk, представляющие количество случаев появления соответствующей прочности.
Для построения опытной кривой производят статистическую обработку результатов испытаний, в ходе которой определяют:
- среднеарифметическое значение прочности
 (2.10)
(2.10)
- среднеквадратическое отклонение (стандарт), характеризующее разброс прочности относительно среднего значения
 (2.11)
(2.11)
где D1 = R 1 – Rm; D2 = R 2 – Rm; …, D k = Rk – Rm - отклонения отдельных значений прочности от среднего значения;
- коэффициент вариации (изменчивости) прочности бетона в партии, который характеризует степень рассеяния прочности бетона
 (2.12)
(2.12)
Весь размах наблюдений Rmin – Rmax разбивают на ряд интервалов и строят гистограмму (а если соединять середины интервалов, то получится опытная кривая).
Кривые распределения прочности бетона (и арматуры) как правило, симметричны относительно среднего значения и хорошо описываются теоретической кривой нормального распределения случайной величины (в нашем случае – прочности бетона). Следует отметить, что теоретические кривые распределения прочностных характеристик асимптотически приближаются к оси абсцисс, не пересекая ее, так что в принципе не существует определенной граничной, минимальной или максимальной величины прочности материала.
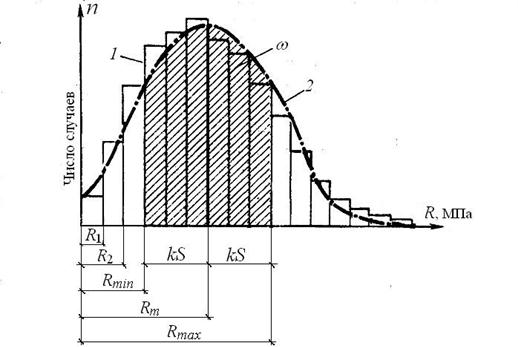
Рис. 13. Гистограмма (1) и теоретическая кривая (2) распределения прочности бетона
Отношение площади w, ограниченной кривой распределения и осью абсцисс на длине участка Rmax – Rmin, ко всей площади, ограниченной кривой распределения (от -¥ до +¥), является вероятностью непоявления значений прочности больше Rm + kS и меньше Rm – kS. Чем больше число k стандартов, тем больше площадь w и тем больше вероятность непоявления прочности, равной Rmax и Rmin, (т.е. тем выше надежность), но значения Rmax и Rmin будут уменьшаться с увеличением числа k.
Следовательно, наименьшее вероятное значение прочности бетона с заданной (через число k стандартов) обеспеченностью отстоит от среднего значения
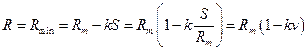 . (2.13)
. (2.13)
Число k – показатель надежности, зависящий от заданной обеспеченности (доверительной вероятности) Р наименьшего значения прочности:
k = 1 – P = 0,84 (84% всех образцов покажут прочность не ниже Rmin);
k = 1,64 – P = 0,95 (95% - “ – “ – ‘ – “ – “ – “ – “ – “ – “ – “ – “ – “ – “ – “ -);
k = 3 – P = 0,997 (99,7% - “ – “ – ‘ – “ – “ – “ – “ – “ – “ – “ – “ – “ – “ – “ -).
Нормами проектирования установлена обеспеченность P = 0,95, а коэффициент вариации v = 0,135. Тогда по (2.13) наименьшее контролируемое значение временного сопротивления сжатию или класс бетона по прочности на сжатиеB (иначе – нормативная кубиковая прочность Rn)
B º Rn = Rmin = Rm (1 – 1,64 v) (2.14)
или B = Rm (1 – 1,64×0,135) = 0,778 Rm,
где Rm – среднее значение кубиковой прочности.
Класс бетона по прочности на осевое растяжение Bt назначают так же, но при значении коэффициента вариации v = 0,165 (т.к. разброс прочности на растяжение больше, чем на сжатие) и только для конструкций, в которых он имеет решающее значение (резервуары, водонапорные трубы, силосы) и контролируется на производстве. Нормы устанавливают следующий параметрический ряд классов бетона по прочности на осевое растяжение:
Вt0,8; Вt1,2; Вt1,6, Вt2,0; Вt2,4; Вt2,8; Вt3,2.
Марки бетона характеризуют его физические свойства. Нормы устанавливают марки тяжелого бетона по следующим показателям:
по морозостойкости – F50; F75; F100; F150; F200; F300; F400; F500 (количество циклов попеременного замораживания и оттаивания водонасыщенных образцов, испытанных в соответствии с ГОСТ, при котором прочность снижается не более чем на 15%);
по водонепроницаемости – W2; W4; W6; W8; W10; W12 (наибольшее давление воды, МПа, при котором не наблюдается ее просачивание через бетон стандартного образца, испытанного в соответствии с ГОСТ;
по средней плотности (кг/м3): для тяжелых бетонов – D2300, D2400, D2500; для легких – от D800 до D2000.
Для любых материалов, помимо данных о прочности, необходимо иметь характеристики деформативности, с помощью которых можно определять смещения.
Деформативность твердых тел – их свойство изменять форму и размеры под действием силовых и несиловых факторов. Деформации разделяют на силовые и несиловые. Силовые деформации возникают при действии внешних сил, развиваются в направлении действия этих сил и проявляются в виде деформаций сжатия, растяжения, сдвига. Силовым продольным деформациям также соответствуют поперечные деформации.
Несиловые деформации (усадка, набухание, температурные воздействия) являются объемными и развиваются одинаково во всех направлениях.
Силовые деформации в зависимости от характера приложения нагрузки и длительности ее действия подразделяются на три вида:
- при однократном нагружении кратковременной нагрузкой;
- при длительном действии нагрузки;
- при многократно повторном действии нагрузки.
Связь между деформативными и прочностными характеристиками бетона устанавливается с помощью диаграмм «напряжения – деформации» (sb - eb), получаемых при испытаниях на осевое сжатие бетонных призм.
5.1. Деформации бетона при однократном кратковременном загружении. Бетонная призма с установленными приборами или наклеенными тензодатчиками для замера деформаций (рис. 14, а) загружается по ступеням величиной 0,1…0,2 от ожидаемой разрушающей нагрузки. На каждой ступени деформации замеряются дважды: первый раз – сразу после приложения нагрузки, второй – после выдержки в 5 – 7 минут под нагрузкой. График в координатах «sb – eb» представляет ступенчатую линию (рис. 14, б). Деформации, измеренные сразу после приложения нагрузки, упругие eе, подчиняющиеся закону Гука (линейная зависимость деформаций от напряжений); деформации, развивающиеся за время выдержки под нагрузкой, неупругие epl и на графике представлены горизонтальными площадками. Следовательно, полная деформация бетона на каждой ступени складывается из упругой ee = sb / Eb (восстанавливающейся) и неупругой epl = f (t, sb / Rb, B) (не восстанавливающейся после разгрузки):
eb = ee + epl. (2.14)
При достаточно большом количестве ступеней нагружения зависимость «sb – eb» можно изобразить плавной кривой (рис. 14, 15).
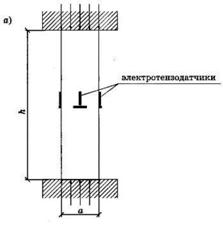
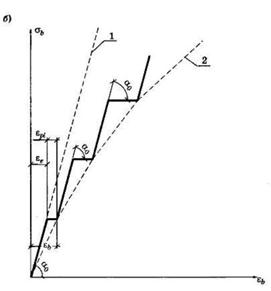
Рис. 14. Определение продольных деформаций бетона при сжатии:
а – опытный образец (призма) с наклеенными электротензодатчиками; б – опытная диаграмма sb – eb при приложении нагрузки ступенями; 1 – прямая упругих деформаций; 2 – кривая полных деформаций
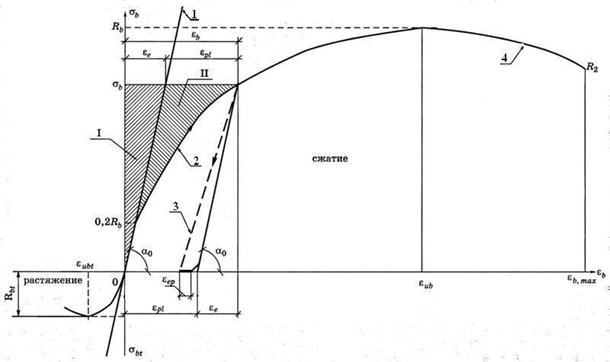
Рис. 15. Диаграмма sb – eb при сжатии и растяжении:
I – область упругих деформаций; II – область неупругих деформаций; 1 – прямая упругих деформаций;
2 - восходящая ветвь диаграммы; 3 – разгрузка; 4 – нисходящая ветвь диаграммы; ebu – предельная сжимаемость; ebtu – предельная растяжимость; eb , max – максимальная сжимаемость при нисходящей ветви диаграммы
Из диаграммы видно, что при малых напряжениях (sb £ 0,2 Rb) бетон деформируется линейно как упругий материал, подчиняющийся закону Гука. При напряжениях sb > 0,25 Rb в бетоне возникают неупругие (нелинейные) деформации (часто их называют пластическими), которые развиваются во времени и зависят от скорости приложения нагрузки и уровня напряжений sb / Rb. Все же при напряжениях в бетоне sb £ 0,5 Rb превалируют упругие деформации (ee ³ 0,8 eb).
При напряжениях sb ³ 0,5 Rb неупругие деформации нарастают более интенсивно (что связано и с развитием микротрещин), кривая«sb – eb» становится более пологой, полные деформации eb увеличиваются.
Если в какой-то момент загружения, соответствующий sb, нагрузку снять, произойдет разгрузка. После полной нагрузки в образце сохраняются накопленные неупругие деформации. Небольшая доля остаточных деформаций (около 10%) в течение некоторого времени после разгрузки восстанавливается (eep на рис. 15) и называется деформацией упругого последействия.
К концу нагружения, когда напряжения sb превосходят верхнюю границу микротрещинообразования 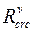 , рост неупругих деформаций резко увеличивается, микроразрушения переходят в макроразрушения и образец разрушается. Если по мере падения сопротивления удается в той же мере снижать нагрузку, то можно получить нисходящую ветвь 4 диаграммы.
, рост неупругих деформаций резко увеличивается, микроразрушения переходят в макроразрушения и образец разрушается. Если по мере падения сопротивления удается в той же мере снижать нагрузку, то можно получить нисходящую ветвь 4 диаграммы.
Деформации бетона ebu, соответствующие максимальным напряжениям Rb на диаграмме sb – eb, характеризуют предельную сжимаемость бетона и колеблятся в пределах 0,001…0,003 в зависимости от класса бетона, его состава, плотности и скорости нагружения.
· Для количественной оценки деформативных свойств используют такие характеристики, как начальный модуль упругости и модуль упругопластичности.
Начальный модуль упругости бетона Eb соответствует только упругим деформациям (т.е. при напряжениях sb £ 0,2 Rb) и равен  . (2.15)
. (2.15)
При напряжениях sb > 0,2 Rb зависимость sb – eb становится нелинейной, модуль в каждой точке диаграммы получается переменным (как тангенс угла наклона касательной 5 к кривой полных деформаций в точке с напряжением sb, рис. 16): 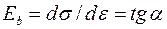 , и определение полных деформаций затруднительно, т.к. общепринятой аналитической зависимости для модуля полных деформаций бетона пока не предложено.
, и определение полных деформаций затруднительно, т.к. общепринятой аналитической зависимости для модуля полных деформаций бетона пока не предложено.

Рис. 16. К определению модуля упругости и модуля упругопластичности:
1 – область упругих деформаций; 2 – область пластических деформаций; 3 – прямая упругих деформаций;
4 – секущая; 5 – касательная; 6 – кривая полных деформаций
Для практических расчетов используется модуль упругопластичности, представляющий тангенс угла наклона секущей 4, проведенной из начала координат диаграммы sb – eb в точку с заданным напряжением sb (см. рис. 16), т.е.
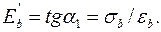 (2.16) Между начальным модулем упругости Eb и модулем упругопластичности
(2.16) Между начальным модулем упругости Eb и модулем упругопластичности  имеется очевидная связь:
имеется очевидная связь:

 откуда
откуда 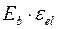 =
= 
и  =
=  (2.17)
(2.17)
где 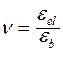 - коэффициент упругости бетона, с увеличением напряжений и продолжительности действия нагрузки значения
- коэффициент упругости бетона, с увеличением напряжений и продолжительности действия нагрузки значения 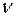 уменьшаются;
уменьшаются;
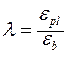 - коэффициент пластичности бетона.
- коэффициент пластичности бетона.
Диапазон изменения этих коэффициентов составляет: 1,0 > n > 0,15; 0,85 ³ l ³ 0.
В практических расчетах начальный модуль упругости тяжелых бетонов естественного твердения рекомендуется определять по формуле
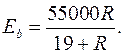 (2.18)
(2.18)
В приложении СНиП 52-01-2003 приведены значения начальных модулей упругости для всех видов и классов бетона.
При осевом растяжении, как и при сжатии, диаграмма sb – eb криволинейна. Начальные модули упругости бетона при растяжении Ebt и при сжатии Eb отличаются незначительно и могут быть приняты одинаковыми (см. рис. 16, 15).
По аналогии вводится понятие модуля упругопластичности, а также коэффициентов упругости и пластичности бетона при растяжении
 . (2.19)
. (2.19)
Если растягивающее напряжение в бетоне приближается к временному сопротивлению осевому растяжению  среднее значение
среднее значение  = 0,5.
= 0,5.
5.2. Деформации бетона при длительном действии нагрузки. При длительном действии нагрузки неупругие деформации с течением времени значительно увеличиваются (рис. 17, а).

Рис. 17. Деформативность бетона во времени:
а – рост деформаций ползучести во времени; б – опытный образец;
в – релаксация (снижение) напряжений в бетоне с течением времени; 1 – связи
Нарастание неупругих деформаций бетона при длительном действии нагрузки называется ползучестью. Природа ползучести бетона объясняется его структурой, длительным процессом кристаллизации и уменьшением количества геля при твердении цементного камня. Наибольшая интенсивность нарастания деформаций ползучести наблюдается в первые 3…4 месяца после загружения, затем рост постепенно замедляется и через несколько лет прекращается. Замечено, что нарастание деформаций ползучести прекращается одновременно с окончанием нарастания прочности бетона.
Деформации ползучести развиваются, главным образом, в направлении действия усилий и могут превышать упругие в 3…4 раза, что заставляет считаться с ними и учитывать при расчете и проектировании железобетонных конструкций.
Ползучесть условно разделяют на линейную и нелинейную. При линейной ползучести зависимость между напряжениями и деформациями ползучести можно считать линейной, что имеет место при напряжениях sb £  (
( - напряжение, соответствующее нижней границе микротрещинообразования), можно считать при sb £ 0,5 R. Линейная ползучесть во времени затухает, асимптотически приближаясь к предельному значению (рис. 18).
- напряжение, соответствующее нижней границе микротрещинообразования), можно считать при sb £ 0,5 R. Линейная ползучесть во времени затухает, асимптотически приближаясь к предельному значению (рис. 18).

Рис. 18. Развитие деформаций ползучести во времени:
а – при разных напряжениях; б – при загружении в различном возрасте
Затухающий во времени характер ползучести обусловлен:
- уменьшением в объеме гелевой (вязкой) структурной составляющей цементного камня (в основном, именно она подвержена ползучести);
- перераспределением напряжений с гелевой составляющей на кристаллический сросток, а с него – на заполнители.
При напряжениях sb >  имеет место нелинейная ползучесть, при которой деформации растут быстрее напряжений. В этом случае, кроме указанных выше явлений, возникают и развиваются микротрещины. Такие необратимые нарушения структуры ведут к ускоренному нарастанию деформаций.
имеет место нелинейная ползучесть, при которой деформации растут быстрее напряжений. В этом случае, кроме указанных выше явлений, возникают и развиваются микротрещины. Такие необратимые нарушения структуры ведут к ускоренному нарастанию деформаций.
Величина деформации ползучести зависит от очень многих факторов. Опыты показывают, что ползучесть увеличивается с повышением содержания цемента и воды; уменьшается - при применении более плотных заполнителей и увеличении влажности среды, снижении температуры среды, увеличении массивности конструкций (масштабный фактор – образцы с меньшими размерами поперечного сечения при прочих равных условиях показывают большую деформацию ползучести).
Определенное влияние на ползучесть оказывают вид напряженного состояния, уровень напряжений в бетоне, возраст бетона к моменту загружения:
- с увеличением напряжения ползучесть возрастает (см. рис. 18, а);
- чем в более позднем возрасте загружается бетон, тем ниже деформации ползучести, т.к. увеличивается и упрочняется кристаллический сросток, количество геля уменьшается, а вязкость его увеличивается.
Для количественной оценки деформаций ползучести служат:
- характеристика ползучести  ;
;
- мера ползучести Ct.
Характеристика ползучести – это отношение деформации ползучести в момент времени t к упругим деформациям в момент загружения t 0:
 (2.20)
(2.20)
Так как jt может меняться от 0 до ¥, удобнее пользоваться коэффициентами пластичности l и упругости n:
 = leb и eel = n eb, тогда jt = l / n. (2.21)
= leb и eel = n eb, тогда jt = l / n. (2.21)
Мера ползучести представляет отношение деформации ползучести, накопившейся к моменту времени t к действующим постоянным напряжениям:
 (2.22)
(2.22)
а т.к.  = leb и
= leb и  =
= 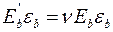 , то
, то
Сt = 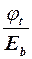 , или
, или  . (2.23)
. (2.23)
Зная меру ползучести, из 2.22 найдем и деформацию ползучести в момент времени t:
 = Ctsb.
= Ctsb.
Предельное значение деформации ползучести можно выразить через предельную меру ползучести  (для времени t
(для времени t  ¥) как
¥) как
 . (2.24)
. (2.24)
Осредненная зависимость предельной меры ползучести от прочности бетона приведена на рис. 19. Зная предельную меру ползучести и постоянные напряжения, по (2.24) легко определить относительные и абсолютные удлинения (укорочения) к моменту стабилизации деформирования t  ¥. Например, толщина швов между элементами облицовки (в направлении сжимающего усилия), прикрепляемой к сжатым граням каменных, бетонных или железобетонных элементов:
¥. Например, толщина швов между элементами облицовки (в направлении сжимающего усилия), прикрепляемой к сжатым граням каменных, бетонных или железобетонных элементов:
 (2.25)
(2.25)
где h – высота облицовки в направлении действия сжимающего усилия.
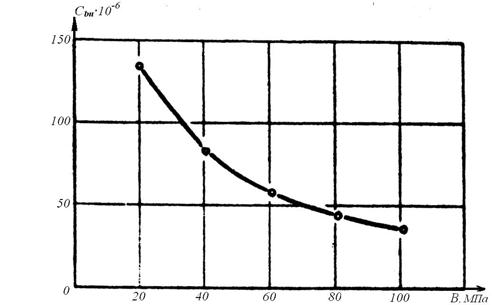
Рис. 19. Зависимость предельной меры ползучести Cbu от класса бетона
при напряжениях в бетоне sb = 0,5 Rb
·С ползучестью тесно связано явление релаксации напряжений, представляющее процесс снижения напряжений во времени при неизменной (зафиксированной) начальной деформации. Если бетонному образцу придать некоторое начальное напряжение sbc и начальную деформацию ebc (рис. 17, б), а затем ввести связи, препятствующие возможности дальнейшего деформирования, то с течением времени напряжения в бетоне будут уменьшаться, стремясь асимптотически к некоторой конечной величине (рис. 17, в). Это свойство обусловливает перераспределение напряжений между бетоном и арматурой (разгружение бетона и нагружение арматуры) во времени, происходящее в сжатых железобетонных элементах.
· Ползучесть и релаксация напряжений бетона (реологические свойства бетона) оказывают существенное влияние на работу железобетонных конструкций при длительном действии нагрузки. Эти свойства обусловливают рост прогибов, снижают предварительные напряжения в арматуре, способствуют перераспределению усилий в железобетонных статически неопределимых системах.
5.3. Усадка бетона. Бетон обладает свойством уменьшаться в объеме при твердении в воздушной среде (усадка) и увеличиваться при увлажнении (набухание). Усадка, как и ползучесть, развивается во времени (рис. 20, б). б
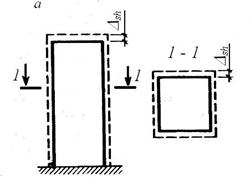

Рис. 20. Деформации усадки бетона:
а – объемный характер усадки бетона; б – развитие усадки и набухания бетона и железобетона во времени;
Различают усадку обратимую, связанную с испарением свободной воды в цементном камне и обусловленную капиллярными явлениями (натяжение менисков в порах бетона), и необратимую, происходящую в результате потери химически связанной влаги на гидратацию цемента и, как следствие, уменьшение объема геля.
Усадка происходит наиболее интенсивно в начальный период твердения и в течение первого года, а затем затухает (рис. 20,б). Зависит она от ряда факторов:
- количество и вид цемента (чем больше цемента на единицу объема бетона, тем больше усадка);
- количество воды (чем больше В/Ц, тем больше усадка);
- влажность среды твердения бетона (чем больше влажность, тем меньше усадка);
- крупность и вид заполнителей (при мелкозернистых песках и пористых заполнителях усадка больше) и другие.
Неравномерное по объему высыхание бетона приводит к неравномерной усадке, что ведет к образованию начальных усадочных трещин. Действительно, открытые поверхностные слои высыхают быстрее и усадка их больше, чем во внутренних, более влажных зонах. Такая неравномерность вызывает во внутренних слоях сжимающие, а в наружных – растягивающие напряжения, приводящие к образованию поверхностных трещин в еще неокрепшем бетоне.
Таким образом, усадка в целом является причиной возникновения в бетоне «собственных» начальных напряжений, которые могут понижать трещиностойкость и жесткость конструкций. В предварительно напряженных конструкциях усадка бетона вызывает потери предварительного напряжения арматуры.
Уменьшение усадочных напряжений достигается мерами:
- технологическими (уменьшение количества цемента и В/Ц, повышение плотности бетона, увлажнение открытых поверхностей, применение безусадочных цементов);
- конструктивными (устройством усадочных швов в конструкциях, постановкой противоусадочной арматуры).
Средние значения деформации усадки тяжелого бетона составляют (2…4)×10-4, т.е. укорочение составляет 0,2…0,4 мм/м.
5.4. Деформации бетона при многократно повторной нагрузке.
Зависят от величины сжимающих напряжений в бетоне. При напряжениях sb £ Rbf (ниже предела выносливости бетона) после достаточно большого количества циклов нагрузка-разгрузка неупругие деформации постепенно выбираются и бетон начинает работать упруго. В этом случае число циклов загружений может быть практически неограниченным без снижения прочности бетона.
При напряжениях sb > Rbf диаграмма sb – eb сначала выпрямляется (прямая 4 на рис. 21), а затем начинает искривляться все больше и больше, но уже в обратном направлении (кривая 5, 6, рис. 21), т.е. происходит неограниченное нарастание неупругих деформаций вследствие нарушений структуры бетона (в частности, образования микротрещин) и затем наступает хрупкое разрушение бетона.

Рис. 21. Зависимость между деформациями и напряжениями при повторных нагружениях:
3 – первичное нагружение; 4 – 675 циклов; 5 – 10,5×104 циклов; 6 – 34,1×104 циклов
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 5352; Нарушение авторских прав?; Мы поможем в написании вашей работы!