
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция II
|
|
|
|
Вывод,
1)Точность вычисления С.К.П. в этом случае достигает 25% от её величины.
2)При восьми измерениях можно получить надёжный результат вычислений по
формуле.
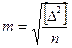
3)Для более точных измерений углов необходимо использовать теодолиты большей
точности.
3. По величине С.К.П. можно определить предельную погрешность 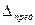 , которая может иметь при данных условиях измерений.
, которая может иметь при данных условиях измерений.
В теории вероятностей доказывается, что при достаточно большом числе измерений
случайная погрешность может быть: 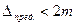 с вероят. 0,950
с вероят. 0,950
— больше 2m в 5 случаях из 100 измерений.
— больше Зm в 3 случаях из 1000 измерений.
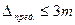 с вероят. 0,0997
с вероят. 0,0997
Поэтому можно принять

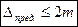 или
или 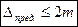
2m— устанавливают при высокоточных измерениях
3m — в остальных случаях.
Выводы:
1)Исходя, из указанных достоинств С.К.П. принимается для оценки геодезических
измерений в качестве основной меры точности.
2)Характеризуя точность измерения С.К.П. (ш), необходимо также указывать и С.К.П.
(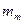 ) вычисления С.К.П.
) вычисления С.К.П.
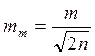
3)Числовые значения средней, С.К.П., и предельной погрешности достаточно вычислять с
двумя значащими цифрами.
(т =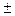 0,35 или т =
0,35 или т =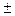 2,3)
2,3)
4)Среднюю С.К.П., 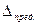 погрешность называют абсолютными погрешностями, т.к. на их
погрешность называют абсолютными погрешностями, т.к. на их
значение не влияет величина измеряемой величины.
Относительная погрешность
используется в тех случаях, когда на точность измерения влияет и размер определяемой
величины.
Рассмотрим результаты измерений двух линий:
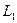 = 350,10м.
= 350,10м. 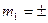 0,35м.
0,35м.
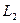 = 800,25м.
= 800,25м. 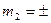 0,40м.
0,40м.
Рассмотрим:
а) абсолютные погрешности измерений:
- 1-я линия измерена точнее, чем вторая, т.к. 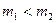
б) вторая линия длиннее первой и очевидно погрешность измерения линии будет зависеть
от её длины.
Поэтому для оценки точности длин линий пользуются относительной погрешностью.
Относительная погрешность — выражает отношение абсолютной погрешности измерения
(m или 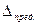 ) к значению самой измеряемой величины.
) к значению самой измеряемой величины.
Относительную погрешность обычно представляют дробью, числитель которой равен 1, а
знаменатель частное отделение длины линии на абсолютную погрешность.
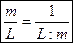
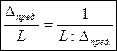
Оценка измерений длин линий.
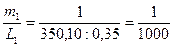
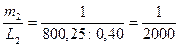
Вывод:
- вторая линия измерена точнее первой, хотя 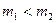
- относительные погрешности не применяют при оценке точности угловых измерений,
поскольку погрешность измерения угла, не зависит от его величины.
Арифметическая середина и оценка её точности.
Имеет ряд равноточных измерений величины и её истинное значение, т.е.:
- 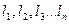
- Х.
Согласно определению случайной погрешности
(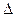 =1-Х) или (1-Х=
=1-Х) или (1-Х=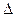 )
)
можно написать для ряда случайных погрешностей
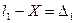
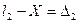
………….
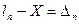
Сложим почленно эти равенства
[l] —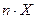 = [
= [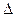 ]
]
после чего разделим их на n измерений
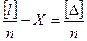
обозначим
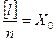
Величина 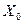 является арифметической серединой или средним арифметическим из
является арифметической серединой или средним арифметическим из
результатов измерений 1, тогда
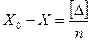 или
или 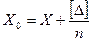
Вывод.
1)Так согласно 3-го свойства случайных погрешностей равноточных измерений 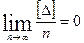 , то арифметическая середина стремится к истинному значению при возрастании числа измерений
, то арифметическая середина стремится к истинному значению при возрастании числа измерений
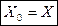
2)На практике выполняют небольшое количество измерений. Тем не менее, и в этих
случаях принято считать арифметическую середину из равноточных измерений наиболее
надёжным результатом таких измерений.
Отклонения, или вероятнейшие погрешности.
Истинное значение измеряемой величины, как правило неизвестно.
Поэтому случайные погрешности 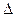 не могут быть вычислены по формуле
не могут быть вычислены по формуле
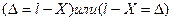 ,
,
а значит не может быть вычислена и С.К.П. отдельного измерения по формуле 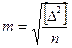 .
.
Тогда оценку точности измерений проводят по отклонениям или вероятнейшим погрешностям отдельных измерений от арифметической середины:

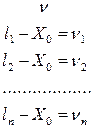
Для установления свойств отклонений:
- сложим почленно эти равенства
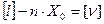
- разделим почленно на n
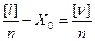
- так как 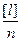 = X0 или
= X0 или 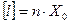
поэтому 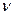 =0
=0
Сумма отклонений 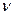 измеренных значений
измеренных значений  от арифметической середины
от арифметической середины 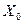 равна нулю. Отклонение
равна нулю. Отклонение 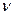 называется вероятнейшими погрешностями.
называется вероятнейшими погрешностями.
По отклонениям 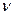 вычисляют С.К.П. отдельного измерения по формуле Бесселя.
вычисляют С.К.П. отдельного измерения по формуле Бесселя.
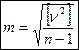
(n-1)- число избыточных измерений
Кроме того, необходимо вычислить:
1)С.К.П. 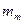 самой С.К.П. m в этом случае определяется по формуле
самой С.К.П. m в этом случае определяется по формуле
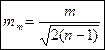
2)С.К.П. М арифметической середины вычисляют по формуле
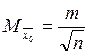
где:
-m-С.К.П.отдельного измерения
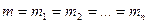
-n число равноточных измерений.
Формула 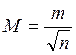 С.К.П. арифметического среднего, даёт возможность сделать практический вывод о том, что повышение точности путём многократных измерений
С.К.П. арифметического среднего, даёт возможность сделать практический вывод о том, что повышение точности путём многократных измерений
одной и той же величины, выгодно только при небольшом числе измерений.
т =10”
Пример n=1;2;4;6;8;
М = 10”;7”;1”;4”;1”.
Поэтому в полевых геодезических работах средней точности число повторений не
превышает 3-4 приемов.
Для существенного повышения точности нужно применить более точные приборы.
Вывод С.К.П. арифметической середины в 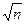 раз меньше С.К.П. отдельного
раз меньше С.К.П. отдельного
измерения.
3)С.К.П. 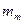 самой С.К.П. М находят по формуле
самой С.К.П. М находят по формуле
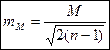
Средние квадратические погрешности Функций измеренных величин.
В практике измерений, часто приходится пользоваться величинами, которые не измеряются, а определяются на основании измеренных величин, т.е, являются некоторыми функциями.
Во всех таких случаях возникает задача вычислений С.К.П. функций, по известным С.К.П. измеренных величин (аргументов).
1)Дано U=х+у погрешности аргументов 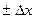 и
и 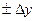
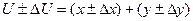
если каждый аргумент измерялся и раз. 
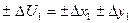
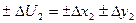
…………………….
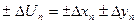
возведем равенства в квадрат и просуммируем

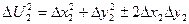
……………………………..
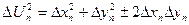
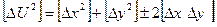
Разделив обе части на n
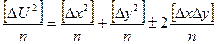 т.к.
т.к. 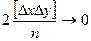
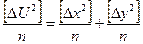 согласно
согласно 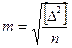
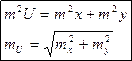
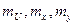 -С.К.П. функции и аргументов.
-С.К.П. функции и аргументов.
Рассуждая аналогично, можно показать, что выражение 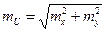 справедливо и для функции u=x-y, а если
справедливо и для функции u=x-y, а если 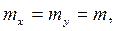 то
то 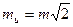 .
.
2) U=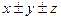
обозначив 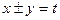 то
то 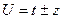 на основании
на основании 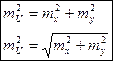
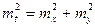
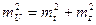
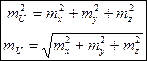 , если
, если 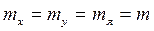
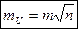
С.К.П. функций измеренных величин.
| Вид функции | С.К.П. | Примеры применения | ||||
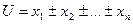
| 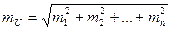 при
при 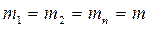
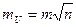
| 1)С.К.П. измерения линии мерной лентой –m-С.К.П. отложения одной ленты
-n-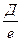 2)С.К.П. определения превышения n при геометрическом нивелировании
- ma
- mb
2)С.К.П. определения превышения n при геометрическом нивелировании
- ma
- mb
| ||||
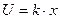
| 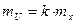
| 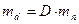 С.К.П. измерения расстояния нитяным дальномером
С.К.П. измерения расстояния нитяным дальномером
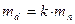 k=100
k=100
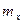 =3мм.(С.К.П. отсчета взятого по рейке) =3мм.(С.К.П. отсчета взятого по рейке)
| ||||
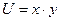
| 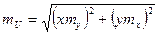
| Определение С.К.П. площади прямоугольника
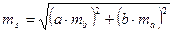

| ||||
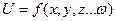
| 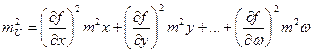
|
З.Неравноточные измерения.
Измерения, выполненные с различной точностью, в различных условиях.
Степень надёжности результатов измерений выражают числом, называемым весом этого
результата.
ЧЕМ НАДЕЖНЕЕ РЕЗУЛЬТАТ, ТЕМ БОЛЬШЕ ЕГО ВЕС.
Следовательно, вес связан с точностью результат измерений, которая характеризуется
С.К.П.
Поэтому вес результата измерений принимают равным величине обратно
пропорциональной квадрату С.К.П. измерения.
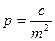
где:
-р- вес результат измерений
-с- произвольное, но одно и тоже число при вычислении всех весов в данной задаче
-m- С.К.П. измерения.
Веса результатов измерений
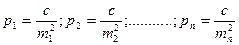
Для облегчения задачи отыскания весов обычно вес одного из результатов с
погрешностью 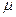 (ми) принимают за единицу и относительно его вычисляют веса
(ми) принимают за единицу и относительно его вычисляют веса
остальных результатов измерений.
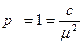 откуда с =
откуда с =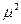
тогда веса результатов наблюдений

За окончательный (наиболее точный) результат и неравноточных измерений равен сумме
произведений каждого из этих измерений на его вес делённый на сумму весов всех
измерений.
 — формула весового среднего или общей
— формула весового среднего или общей
арифметической середины.
Кроме того, необходимо найти:
- уклонения 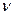 от измеренных величин
от измеренных величин
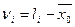
- С.К.П. единицы веса по формуле Бесселя
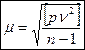
- С.К.П. общей арифметической середины
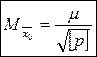
-С.К.П. определения самой средней квадратической погрешности М
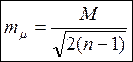
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 371; Нарушение авторских прав?; Мы поможем в написании вашей работы!