Лекция 3. Понятие функции. Виды отображений. Композиция функций. Обратная функция

Пусть заданы непустые множества Х и Y. Соответствие, при котором каждому элементу соответствует единственный элемент 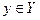, называется функцией, заданной (определенной) на множестве Х со значениями в множестве Y, или отображением множества Х в множество Y. Такая функция обозначается следующим образом:

или .

Наряду с терминами «функция», «отображение» используются равнозначные термины «преобразование», «морфизм».

Элемент х называется независимой переменной, или аргументом, а соответствующий элемент 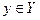- зависимой переменной. Множество Х называется множеством определения функции 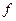, а множество тех 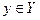, каждый из которых поставлен в соответствие хотя бы одному , - множеством значений функции 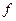и обозначается . Очевидно, 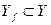. Если 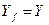, то отображение f называется отображением Х на множество Y, или сюръекцией. Если при выполняется неравенство , то отображение f называется взаимно однозначным отображением Х в Y, или инъекцией. Если f является взаимно однозначным отображением Х на Y, т.е. является одновременно сюръекцией и инъекцией, то оно называется биекцией.

Пусть заданы функция и 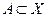. Множество всех 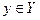, являющихся значениями функции f в точках , называется образом множества А при отображении f и обозначается , т.е. 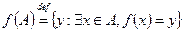. В частности, образом множества Х является множество значений функции .

Если 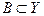, то множество всех тех точек , значения функции f в которых принадлежат множеству В, называется прообразом множества В. То есть, прообразом множества В является множество .

Пусть функция инъективна. Рассмотрим какую-нибудь точку 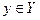. Для этой точки y можно найти такую точку , что 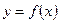. Так как функция f инъективна, то другой точки, удовлетворяющей условию , нет. Поэтому если каждой точке 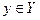мы поставим в соответствие однозначно определенную точку , для которой 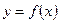, то мы определим на множестве Y некоторую функцию. Введенная таким образом функция называется функцией, обратной функции f, и обозначается символом . Обратную функцию можно определить только для инъективной функции f. Функция определена на множестве f(X) и отображает его на множество Х.

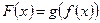Если и , то функция , ставящая в соответствие каждому элементу элемент , называется композицией функций f и g ( суперпозицией, или сложной функцией) и обозначается . Таким образом, согласно определению .

Если функции принимают числовые значения (такие функции называются числовыми или скалярными), то над ними можно производить арифметические операции. Пусть даны две функции и , где X, Y – подмножества множества действительных чисел, тогда, по определению, в каждой точке :

Наглядное представление о числовой функции дает ее график. Это – некоторое множество точек на координатной плоскости, обычно – некоторая линия.

Графиком функции f с областью определения Х называется множество .

Отличительной чертой каждого графика является то, что всякая прямая, параллельная оси ординат (т.е. прямая 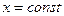) пересекает его не более чем в одной точке.

Для задания функции надо указать множество Х (область определения функции) и описать правило, по которому для данного значения аргумента можно найти соответствующее значение функции. Чаще всего используются следующие три способа задания функции.

1. Табличный. Если область определения является конечным множеством чисел 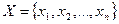, то для задания функции проще всего указать таблицу:

X	x1	x2	…	xn
Y	y1	y2	…	yn

Примерами могут служить таблицы расписания движения поездов, выигрышей в лотерее и т.п.

2. Аналитический, т.е. задание с помощью формулы, указывающей, какие действия надо произвести над аргументом х, чтобы получить значение функции y. Например, 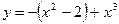. При аналитическом способе не исключается и такое положение, когда функция задается не одной формулой, а с помощью нескольких:

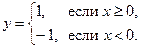
3. Графический, т.е. с помощью графика. Чаще всего используется на практике, когда зависимость y от х вычерчивается прибором. (Например, ЭКГ больного).

Наиболее простые приложения математического анализа ограничиваются кругом так называемых элементарных функций, основными из которых являются следующие:

1. Степенные функции , где а – любое постоянное число.

2. Показательные функции , где а>0, а¹1.

3. Логарифмические функции , где а>0, а¹1.

4. Тригонометрические функции .

5. Обратные тригонометрические функции .

Элементарными функциями называются такие, которые получаются из основных при помощи арифметических действий и композиции функций.

Дата добавления: 2014-01-20