
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос №4. Эквипотенциальные поверхности. Связь между напряженностью и потенциалом
|
|
|
|
Вопрос №3. Потенциал поля точечного заряда и системы точечных зарядов
С учетом выражения (1.4) для потенциала точечного заряда получим:
|


|
Зависимости радиальной проекции напряженности Еr = Е(r) и потенциала φ=φ(r) для положительных и отрицательных точечных зарядов q представлены на (рис. 2а, 2б)соответственно.
Эквипотенциальной поверхностью называется геометрическое место точек поля, имеющих одинаковый потенциал φ, поэтому эти поверхности удовлетворяют условиюφ = const. Из формулы (1.6) следует, что эквипотенциальные поверхности (φ = const) потенциала точечного заряда являются сферами (рис.3), как это и должно быть для центрально-симметричного поля.

|
|
С помощью потенциала φ выражение для работы электростатического поля по перемещению заряда запишем в виде:
|
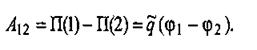
Если электростатическое поле создается не точечным, а любым распределенным зарядом, то все выводы относительно потенциальности поля и работы по перемещению заряда в нем справедливы, т.е. формулы (1.5) и (1.7) остаются в силе. Однако в этом случае выражение для потенциала поля нужно находить с помощью принципа суперпозиции, как при определении напряженности 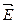 системы зарядов
системы зарядов  :
:

Из определения потенциальной энергии (А12 = П(1) - П(2))следует, что элементарная работа равна убыли потенциальной энергии:  Чтобы получить взаимосвязь между силовой характеристикой
Чтобы получить взаимосвязь между силовой характеристикой 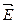 и энергетической характеристикой φ, запишем в развернутом виде левую и правую части этого выражения в координатной форме:
и энергетической характеристикой φ, запишем в развернутом виде левую и правую части этого выражения в координатной форме:
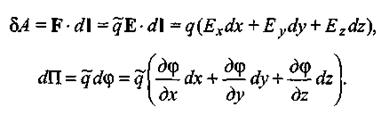
|
Отсюда получаем (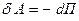 ) выражения для проекций вектора
) выражения для проекций вектора 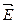 :
:
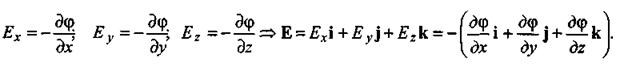
|
Окончательно взаимосвязь между 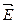 и φ имеет вид:
и φ имеет вид:

|
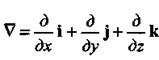 - векторный оператор Гамильтона, или оператор Набла
- векторный оператор Гамильтона, или оператор Набла
Сам по себе этот вектор (оператор) не имеет физического смысла, однако после символического умножения оператора набла на скалярную или векторную функцию получаются выражения, которые имеют вполне определенный физический смысл.
Например, произведение 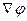 определяет вектор напряженности
определяет вектор напряженности 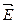 , а скалярное произведение
, а скалярное произведение 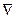 на вектор А (х, у, z) — дивергенцию векторного поля А. В Si напряженность измеряется [Е] =1 В/м = 1 Н/Кл.
на вектор А (х, у, z) — дивергенцию векторного поля А. В Si напряженность измеряется [Е] =1 В/м = 1 Н/Кл.
Задача 1. Определить ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от υ1 =1 м/с до υ2 =5 Мм/с.
Решение:  - работа, совершаемая силами электрического поля при перемещении электрона из одной точки в другую, т.е равна убыли потенциальной энергии. Эта работа идет на увеличение кинетической энергии электрона, т.е.
- работа, совершаемая силами электрического поля при перемещении электрона из одной точки в другую, т.е равна убыли потенциальной энергии. Эта работа идет на увеличение кинетической энергии электрона, т.е.  . приравняв эти формулы получим:
. приравняв эти формулы получим:
 =
= 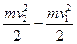 , отсюда
, отсюда  .
.
Подставив числовые значения получим:

Задача 2. Пространство между двумя концентрическими сферами радиусы которых R1 и R2 , заряжено плотностью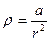 (а = const, r – расстояние от центра сферы до точки наблюдения). Найти полный заряд q, а также напряженность поля E и потенциал φ для r< R1..
(а = const, r – расстояние от центра сферы до точки наблюдения). Найти полный заряд q, а также напряженность поля E и потенциал φ для r< R1..
Решение: для нахождения полного заряда выделим в пространстве между сферами очень тонкий сферический слой(см. рис.4) толщиной dr. Заряд этого слоя равен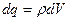 . Объем слоя
. Объем слоя  .
.
 Рис. 4
Рис. 4
Полный заряд q найдем интегрированием по r от R1 до R2:

Для нахождения напряженности поля Е в случае r< R1 применим теорему Гаусса. Напряженность Е0 в случае r< R1, т.к. феерическая повепрхность радиуса r< R1, сквозь которую подсчитываем поток вектора  , зарядов не охватывает. Потенциал в этой области постоянен, т.к.
, зарядов не охватывает. Потенциал в этой области постоянен, т.к. 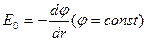
Задача 3. Найти потенциал точки поля, находящейся на расстоянии r1=0,1м от поверхности шара радиусом и r2=0,03, имеющего поверхностную плотность заряда σ = 10-5 Кл/м2.
Решение:  ; q = σS (
; q = σS (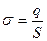 )
)
q =  (Кл)
(Кл)
r = r1+ r2 =0,1 + 0,03 = 0,13(м) –расстояние от центра шара до точки поля, потенциал которой определяется.
Следовательно: 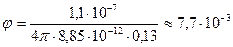 (В).
(В).
Задача 4. Два одноименных точечных заряда q1 = 10-7 Кл и q2=2·10-7 Кл находятся на расстоянии r1=0,8 м друг от друга. Какую работу надо совершить, чтобы сблизить их до расстояния r2 = 0,2 м?
Решение: пусть заряд q2 перемещается в поле заряда q1. При этом совершается работа  . Т.к.
. Т.к.  и
и  , то
, то
А= q2· (
 -
-  ) =
) =  (Дж).
(Дж).
Задача 5. Какую скорость приобретает электрон, перемещаясь в электрическом поле между точками с разностью потенциалов 6,2В?
Решение: А =  (Дж).
(Дж).
А – работа при перемещении электрона в электрическом поле. В результате этой работы электрон приобретает кинетическую энергию 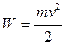 , а т.к. А = W, то (м/
, а т.к. А = W, то (м/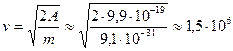 с)
с)
Литература:
1. И.И. Наркевич, Э.И. Волмянский, С.И.Лобко. Физика. – Мн.: 0.0.0. «Новое знание», 2004.
2. А.Н. Ремизов. Курс физики, Электроники и кибернетики. – М.: Высшая ШК., 1982.
3. П.С. Кудрявцев. Курс истории физики. – М.: Просвещение, 1974.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1510; Нарушение авторских прав?; Мы поможем в написании вашей работы!