Методы моделирования детерминированных факторных систем

Одной из основных задач факторного анализа является моделирование взаимосвязей между различными показателями и факторами, которые определяют их величину.

Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения.

Моделирование мультипликативных факторных систем в АДХДП осуществляется путем последовательного расчленения факторов исходной системы на факторы сомножители.

Например, при исследовании формирования объема производства продукции можно применить такие детерминированные модели:

ВП=ЧР*ГВ;

ВП=ЧР*Д*ДВ;

ВП=ЧР*Д*П*ЧВ,

Где:

ВП – валовая продукция;

ЧР – численность рабочих;

ГВ – годовая выработка 1 среднесписочного рабочего;

Д – количество дней отработанных за год;

ДВ – дневная выработка 1 среднесписочного рабочего;

П – средняя продолжительность рабочего дня (ч);

ЧВ – среднечасовая выработка одного рабочего.

Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Моделирование аддитивных факторных систем осуществляется аналогично мультипликативным, т.е. путем расчленения факторов исходной модели на составные элементы.

Например:

VРП=VВП-О_НП,

Где:

VВП – объем производства;

О_нп – остаток нереализованной продукции.

Более детально:

VВР=VВП-О_скл.-О_отг

Где:

О_скл – продукция на складе предприятия;

О_отг – продукция отгруженная, но не оплаченная покупателями.

Применительно к классу детерминированных факторных систем различают следующие основные приемы моделирования.

Метод удлинения факторной системы предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Исходная факторная система 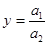. Если а₁ представить в виде суммы отдельных слагаемых-факторов а₁=а₁₁+а₁₂+….+а_1n, то 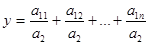- конечная факторная система вида .

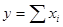Например, себестоимость единицы продукции можно представить в виде функции двух факторов: изменение сумы затрат (З) и объема выпуска продукции (Q_ВП). Исходная модель системы будет иметь вид:

С=З/Q_ВП

Если общую сумму затрат (З) заменить отдельными их элементами, такими как оплата труд (ОТ), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (НР) и т.д., то получим аддитивную модель с новым набором факторов:

С=ОТ/ Q_ВП+СМ/ Q_ВП+А/ Q_ВП+НР/ Q_ВП=x₁+x₂+x₃+x₄

Где:

x₁ – трудоемкость продукции;

x₂ – материалоемкость;

x₃ – фондоемкость;

x₄ – уровень накладных затрат.

Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Исходная факторная система 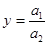. Если числитель, и знаменатель дроби «расширяется» умножением на одно и то же число, то получим новую факторную систему:

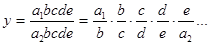, т.е. мультипликативную модель вида .

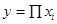Этот способ моделирования широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ=ВП:ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (Д_общ), то получим следующую модель годовой выработки:

ГВ=(ВП* Д_общ)/(ЧР* Д_общ)=(ВП Д_общ)*(Д_общ/ЧР)=ДВ*Д,

Где:

ДВ – среднедневная выработка;

Д – количество отработанных дней одним работником.

Метод сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на одни и тот же показатель. В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов. Исходная факторная система 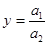. Если числитель и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему (при этом, естественно, должны быть соблюдены правила выделения факторов):

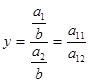
В данном случае имеем конечную факторную систему вида

Как известно, рентабельность совокупных активов предприятия рассчитывается делением суммы прибыли (П) на из среднегодовую стоимость (А):

R=П/А.

Если числитель и знаменатель разделим на выручку (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:

R=П/А=(П:В)/(А:В)=Рентабельность продаж/Капиталоемкость продукции.

Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя.

Рассмотренные модели отражают процесс последовательной детализации влияния факторов на изменение объема продукции как обобщающего показателя. Аналогичные модели могут быть построены и для других показателей хозяйственной деятельности.

В основе детерминированного моделирования факторной системы лежит возможность построения тождественного преобразования для исходной формулы экономического показателя по теоретически предполагаемым прямым связям последнего с другими показателями-факторами. Детерминированное моделирование факторных систем – это простое и эффективное средство формализации связи экономических показателей; оно служит основной для количественной оценки роли отдельных факторов в динамике изменения обобщающего показателя.

Детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей. При недостаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности часто необходим иной подход к познанию объективной действительности. Размах количественных изменений экономических показателей можно выяснить только стохастическим анализом массовых эмпирических данных.

Стохастический анализ направлен на изучение косвенных связей, т.е. опосредованных факторов (в случае невозможности определения непрерывной цепи прямой связи). Из этого вытекает важный вывод о соотношении детерминированного и стохастического анализа: так как прямые связи необходимо изучать в первую очередь, то стохастический анализ носит вспомогательный характер. Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.

Стохастическое моделирование факторных систем взаимосвязей отдельных сторон хозяйственной деятельности опирается на обобщение закономерностей варьирования значений экономических показателей – количественных характеристик факторов и результатов хозяйственной деятельности. Количественные параметры связи выявляются на основе сопоставления значений изучаемых показателей в совокупности хозяйственных объектов или периодов. Таким образом, первой предпосылкой стохастического моделирования является возможность составить совокупность наблюдений, т.е. возможность повторно измерить параметры одного и того же явления в различных условиях.

При детерминированном факторном анализе модель изучаемого явления не изменяется по хозяйственным объектам и периодам (так как соотношения соответствующих основных категорий стабильны). При необходимости сравнения результатов деятельности отдельных хозяйств или одного хозяйства в отдельные период может возникать лишь вопрос о сопоставимости выявленных на основе модели количественных аналитических результатов. В стохастическом анализе, где сама модель составляется на основе совокупности эмпирических данных, предпосылкой получения реальной модели является совпадение количественных характеристик связей в разрезе всех исходных наблюдений. Это означает, что варьирование значений показателей должно происходить в пределах однозначной определенности качественной стороны явлений, характеристиками которых являются моделируемые экономические показатели (в пределах варьирования не должно происходить качественного скачка в характере отражаемого явления). Следовательно, второй предпосылкой применяемости стохастического подхода к моделированию систем является качественная однородность совокупности (относительно изучаемых связей).

Изучаемая закономерность изменения экономических показателей (моделируемая связь) выступает в скрытом виде. Она переплетается со случайными с точки зрения исследования (неизучаемыми) компонентами вариации и ковариации показателей. Закон больших чиселл гласит, что только в большой совокупности закономерная связь выступает устойчивее случайного совпадения направления варьирования (случайной ковариации). Из этого вытекает третья предпосылка стохастического анализа – достаточная размерность (численность) совокупности наблюдений, позволяющая с достаточной надежностью и точностью выявить изучаемый закономерности (моделируемые связи). Уровень надежности и точности модели определяется практическими целями использования модели в управлении производственно-хозяйственной деятельностью.

Четвертая предпосылка стохастического подхода –наличие методов, позволяющих выявить количественные параметры связей экономических показателей из массовых данных варьирования уровня показателей. Математический аппарат применяемых методов иногда предъявляет специфические требования к моделируемому эмпирическому материалу. Выполнение данных требований является важной предпосылкой применяемости методов и достоверности полученных результатов.

Основная особенность стохастического факторного анализа заключается в том, что при стохастическом анализе нельзя составлять модель путем качественного (теоретического) анализа, необходим количественный анализ эмпирических данных.

В экономических исследованиях нашили применение следующие математико-статистические методы стохастического моделирования хозяйственных явлений и процессов; оценка статистической значимости связей; регрессионный анализ; выявление параметров периодических колебаний экономических показателей; группировка многомерных наблюдений; дисперсионный анализ; современный факторный (компонентный) анализ; трансформационный анализ.

5. Функционально-стоимостной анализ. SWOT –анализ.

Дата добавления: 2014-01-20