
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ №3 часть 2
|
|
|
|
Профилактика.
Лечение.
Розовые угри
Этиология:
- ангионевротические расстройства,
- желудочно-кишечные заболевания,
- переохлаждение,
- клещи Demodex folliculorum, находящийся в сальных железах.
- инсоляция,
- прием алкоголя, острых блюд.
Чаще болеют женщины 40-50 лет.
Клиника.
Локализация:
1) кожа носа,
2) средней части лба,
3) щек, бороды.
Заболевание начинается с покраснения и отечности, на фоне которых появляются угревые элементы, узелки, пустулы и телеангиоэктазии.
Клинические формы:
1) эритематозная – стойкая гиперемия с поверхностными телеангиоэктазиями, кожа утолщена, жирная, с расширенными устьями сальных желез;
2) Эритематозно-папулезная- наличие фолликулярных папул красноватого цвета;
3) Папуло-пустулезная;
4) Пустулезно-узловатую, или ринофиму (шишкообразный нос) – бугристые, фиолетового цвета, мягкой консистенции, опухолевидные образования, пустулы, телеангиоэктазии, рубцы.
Общее терапия.
- Установить этиологический фактор и устранить.
- Витаминотерапия вит. гр.В.
- Гипосенсибилизирующая терапия.
- Антибиотики тетрациклинового ряда.
Местное лечение.
Уход за кожей: обмывание кожи лица водой контрастной температуры, протирание льдом из простокваши, настоев трав, овощных и фруктовых соков (арбуза, огурца, ромашки, листьев шалфея и др.)
Глюкокортикоидные мази с антибиотиком, кроме фторированных кортикостероидов, мазь Вилькинсона, полисульфидный линимент с димексидом и трихополом, крем метрогил.
Питание.
Исключить острые, соленые, пряные, копчености, алкоголь, кофе, чай.
Не рекомендуется переедать, нарушать режим питания.
Рекомендованы молочно-растительные продукты.
- Выявление и своевременное лечение заболеваний жкт.
- Избегать длительных пребываний на солнце, ветре.
- При стрессовых ситуациях снимать напряжение седативными препаратами.
- исключать блюда, вызывающих гиперемию кожи.
Сложное сопротивление
В общем случае действия сил на брус в его внутренних поперечных сечениях возникают шесть внутренних силовых факторов
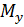 ,
, - изгибающие моменты
- изгибающие моменты
 - крутящий момент
- крутящий момент
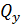 ,
,  – поперечные силы
– поперечные силы
N- продольная сила.
При совместном действии данных силовых факторов брус испытывает сочетание простых видов деформации (растяжение-сжатие, сдвиг, кручение, изгиб).
Сочетание двух и более простых видов деформации бруса - называется сложным сопротивлением.
Распространенными случаями сложного сопротивления бруса являются:
1. косой изгиб,
2. изгиб с растяжение или сжатием,
3. изгиб с кручением,
4. кручение с растяжением или сжатием.
Рассмотрим эти случаи последовательно.
Косой изгиб
Определение. Косым изгибом называется такой вид деформации, при котором плоскость действия суммарного изгибающего момента в сечении, не совпадает ни с одной из главных плоскостей инерции (т.е. изгиб в двух плоскостях).
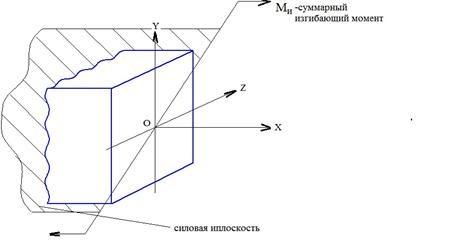
Косой изгиб бывает плоский и пространственный. При плоском косом изгибе все нагрузки располагаются в одной плоскости, не совпадающей с главными плоскостями инерции бруса. При этом изогнутая ось бруса является плоской кривой.
Пример плоского косого изгиба

Силы и нагрузки проходят через ось балки и перпендикулярны оси.
При плоском косом изгибе могут действовать и моменты, но в той же плоскости.
При пространственном косом изгибе нагрузки располагаются в различных плоскостях, проходящих через ось бруса. В этом случае ось бруса является пространственной кривой.
Пример пространственного косого изгиба

Напряжения при косом изгибе
Рассмотрим консольный брус прямоугольного поперечного сечения нагруженной сосредоточенной силой P на свободном конце. Сила Р располагается в плоскости YOZ и наклонена к оси Y под углом α.
Имеем плоский косой изгиб.

Разложим силу Р на составляющие относительно главных осей


Таким образом, косой изгиб приводится к двум прямым изгибом.
Покажем какие усилия действуют в произвольном сечении бруса. Воспользуемся правилом РОЗУ. Оставим часть с заделкой.
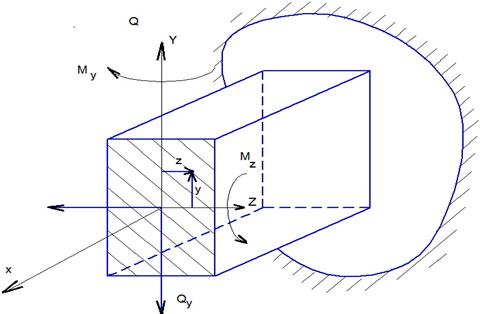
 - вызывает растяжение верхних волокон,
- вызывает растяжение верхних волокон,

 , т. к Р. - проходит через центр тяжести сечения, N=0
, т. к Р. - проходит через центр тяжести сечения, N=0
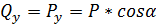
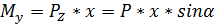
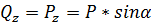

Таким образом, при косом изгибе в поперечном сечении бруса может действовать четыре внутренних силовых фактора.
Зная силовые факторы можно перейти к напряжениям.
Возьмем произвольную точку в I четверти с координатами z,y. Определим в этой точке нормальные напряжения используя принцип независимости действия сил.

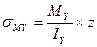

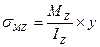
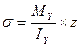 +
+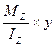 -формула для определения нормальных напряжений для точки с координатами z, y в I четверти.
-формула для определения нормальных напряжений для точки с координатами z, y в I четверти.
Знаки берем из физических соображений, величины берем по модулю.
Если точка в III четверти, то надо взять (-) и (-). Таким образом общая формула должна иметь знаки (±).
В общем виде формула нормальных напряжений при косом изгибе записывается так:
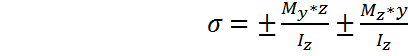 (1)
(1)
Знак перед каждым членом формулы (1) устанавливается из физических соображений (по характеру деформации бруса). y, z, 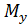 ,
, -берутся по модулю (т.е. по абсолютной величине).
-берутся по модулю (т.е. по абсолютной величине).
Уравнение нейтральной линии при косом изгибе
Нейтральная линия это геометрическое место точек, где нормальное напряжение равно нулю.
Пусть через точку с координатами y, z находящуюся в первой четверти проходит нейтральная линия.
Обозначим координаты ноликом:
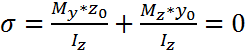 уравнение нейтральной линии при косом изгибе;
уравнение нейтральной линии при косом изгибе;
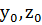 - координаты точки, принадлежащей нейтральной линии.
- координаты точки, принадлежащей нейтральной линии.
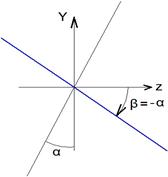
Дадим плоское изображение поперечного сечения β>0 для нашего случая.
tgβ =  = -
= -  (2)
(2)
Было  в первой четверти.
в первой четверти.

В формуле (2) моменты 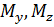 считаются положительными, если они в точках первой четверти вызывают растягивающее напряжение.
считаются положительными, если они в точках первой четверти вызывают растягивающее напряжение.
Нейтральная линия при косом изгибе проходим через центр тяжести сечения и наклонена под углом β и к оси Z.
Силовая линия это след плоскости действия внешних сил (силовой плоскости).
При косом изгибе нейтральная линия (ось) не перпендикулярно силовой линии. А при прямом изгибе нейтральная ось перпендикулярно силовой линии. Нейтральная линия всегда пересекает те четверти осей координат, напряжения в которых от моментов 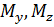 получаются разных знаков.
получаются разных знаков.
Нейтральная и силовая линия пересекают разные четверти осей координат (не уживаются в одной четверти).
Формула (2) справедлива как для плоского, так и для пространственного косого изгиба.
В частном случае при плоском косом изгибе формулу (2) можно представить в другом виде:
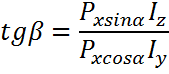
-  (3)
(3)
Для квадрата, круга, любого правильного многоугольника у нас  , то имеем
, то имеем 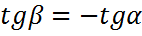 .
. 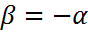 и косого изгиба не имеет места.
и косого изгиба не имеет места.
Эпюры напряжений при косом изгибе в пространственной форме
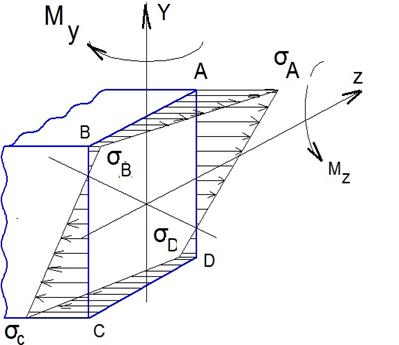

Аналогично 

Сделаем плоское изображение пространственной эпюры  т.к для сложного сечения построить пространственную эпюру сложно.
т.к для сложного сечения построить пространственную эпюру сложно.
Рассмотрим сечение с одной осью симметрии.
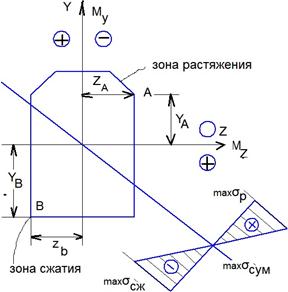
Предположим, что 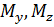 вызывают растяжение в первой четверти. Изобразим направление моментов
вызывают растяжение в первой четверти. Изобразим направление моментов 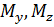 и положение нейтральной оси.
и положение нейтральной оси.
Точки, которые располагаются в наиболее удаленных местах от нейтральной оси - наиболее напряжены.


Построим суммарную эпюру (плоскую) нормальных напряжений. Проведем параллельные нейтральной оси линии через точки А и В и проводим линию перпендикулярную нейтральной оси (базисная линия эпюры  ).
).
Условия прочности при косом изгибе по нормальным напряжениям
В опасных точках сечения касательные напряжения оказываются равными нулю или весьма малы и поэтому при расчетах не учитывается.
Расчет бруса при косом изгибе ведется по нормальным напряжениям.
Наибольшее нормальное напряжение в брусе не должно превышать допустимое нормальное напряжение для материала.
Для пластичных материалов и симметричных сечений условие прочности записываются так
| max | =
| = 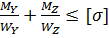 условие прочности для т.А или т.В
условие прочности для т.А или т.В
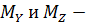 изгибающие моменты в опасном сечении бруса берутся по эпюрам.
изгибающие моменты в опасном сечении бруса берутся по эпюрам.
Для пластичных материалов и несимметричных сечений условие прочности записывается в следующем виде
Пусть |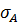 |>|
|>| | | max
| | max | =
| = 
Для материала неодинаково сопротивляющегося растяжению-сжатию записывается два условия прочности.
Одно условие записывается два условия прочности. Одно условие записывается для точки наиболее удаленной от нейтральной оси в растянутой зоне опасного сечения, другое для точки наиболее удаленной от нейтральной оси в сжатой зоне того же сечения.
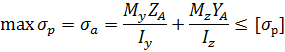
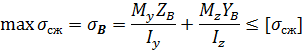
Подбор размеров поперечного сечения при косом изгибе производится путем пробных попыток. Предварительно задаются размером поперечного сечения, и проводит проверку соблюдения условий прочности
max =
= 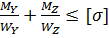
Два неизвестных 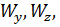 а уравнение одно. Сначала подбирает сечение на чистый изгиб по отдельности
а уравнение одно. Сначала подбирает сечение на чистый изгиб по отдельности 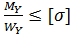 и
и 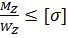 .
.
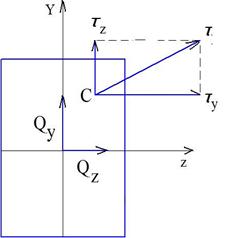
При необходимости определение касательных напряжений, последние вычисляются по формулам Журавского.
Касательные напряжения определяются от  отдельно, а затем складываются геометрически. Найдем
отдельно, а затем складываются геометрически. Найдем  в точке С.
в точке С.
Перемещение при косом изгибе определяются отдельно от сил, действующих в одной главной плоскости инерции и сил, действующих в другой главной плоскости инерции, а затем эти перемещения складываются геометрически.
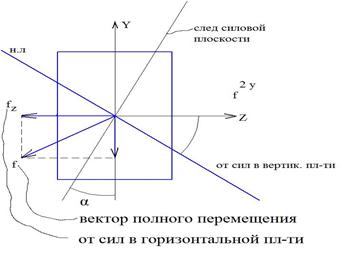
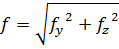
При плоском косом изгибе вектор полного перемещения точки перпендикулярен нейтральной линии и не совпадает с силовой линией.
При пространственном косом изгибе вектор f не перпендикулярен нейтральной линии.
Аналогично вектор полного угла поворота сечения.
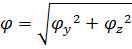
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3505; Нарушение авторских прав?; Мы поможем в написании вашей работы!