Проектирование программ

Современный подход к проектированию программ основан на декомпозиции задачи, которая в свою очередь основана на использовании абстракций. Целью при декомпозиции является создание модулей, которые представляют собой небольшие, относительно самостоятельные программы, взаимодействующие друг с другом по хорошо определенным и простым правилам. Если эта цель достигнута, то разработка отдельных модулей может осуществляться различными людьми независимо друг от друга, при этом объединенная программа будет функционировать правильно.

Различают абстракцию через параметризацию (одним алгоритмом можно решать задачи, отличающихся различными исходными данными, задаваемыми как параметры) и через спецификацию (разными алгоритмами можно получить один и тот же искомый результат. При этом описываются результаты работы программы, смысл обращения к программе становится ясным через анализ ее спецификации, а не самого текста программы.)

Существуют различные подходы и технологии разработки алгоритмов и программ. По взглядам проектирование и разработку программ целесообразно разбить на ряд последовательных этапов:

1. Постановка задачи
   При постановке задачи для крупных компьютерных программ необходимо провести следующие работы:

o Выработать требования (свойства, качества и возможности), необходимые для решения проблемы или достижения цели (как правило, эта деятельность носит экспертный характер);

o Разработать спецификации, включающие

§ Цель программы;

§ граничные условия;

§ описание функций системы;

§ спецификации входных и выходных данных;

§ верификационные требования;

§ тип и количество документов.

В ходе этой работы выявляются свойства, которыми должна обладать система в конечном виде(замысел), описывающий функции системы, характеристики интерфейса.
Чтобы приступить к решению задачи необходимо точно ее сформулировать. В первую очередь, это означает определение исходных и выходных данных, т.е. ответы на вопросы: а) что дано; б) что нужно найти. Дальнейшая детализация постановки задачи представляет собой ответы на серию вопросов такого рода: как определить решение; каких данных не хватает и все ли они нужны; какие сделаны допущения и т.п.

2. Проектирование программы
Сначала производится проектирование архитектуры программной системы. Это предполагает первичную (общую) стадию проектирования и заканчивается декомпозицией спецификаций в структуру системы. Обычно на модульном уровне по каждому модулю разрабатывается спецификация модуля:

o имя/цель - дается имя модулю и предложение о функции модуля с формальными параметрами;

o неформальное описание - обзор действий модуля;

o ссылки - какие модули ссылаются на него и на какие модули ссылается данный модуль

o вход/выход - формальные и фактические параметры, глобальные, локальные и связанные(общие для ряда модулей) переменные;

o примечания - полезные комментарии общего характера по модулю.

Следующим шагом является детальное проектирование. На этом этапе происходит процедурное описание программы, выбор и оценка алгоритма для реализации каждого модуля. Входной информацией для проектирования являются требования и спецификации системы.
Методы проектирования архитектуры делятся на две группы: ориентированные на обработку и ориентированные на данные. Методы, ориентированные на обработку, включают следующие общие идеи:

f. Модульное программирование
Основные концепции:

• каждый модуль реализует единственную независимую функцию;
• имеет единственную точку входа/выхода;
• размер модуля минимизируется;
• каждый модуль разрабатывается независимо от других модулей;
• система в целом построена из модулей.

Исходя из этих принципов каждый модуль тестируется отдельно, затем после кодирования и тестирования происходит их интеграция и тестируется вся система

g. Функциональная декомпозиция
Практически является декомпозицией в форме пошаговой детализации и концепции скрытия информации. Каждый модуль характеризуется субъективным решением проектировщика, связь осуществляется с помощью хорошо организованных интерфейсов.

h. Проектирование с использованием потока данных
Использует поток данных как генеральную линию проектирования программы. Содержит элементы структурного проектирования сверху-вниз с пошаговой детализацией:

§ Экспертиза потоков данных и отображение графа потока данных,

§ Анализ входных, центральных и выходных преобразующих поток данных элементов,

§ формирование иерархической структуры программы,

§ детализация и оптимизация структуры программы.

i. Технология структурного анализа проекта
Основана на структурном анализе с использованием специальных графических иерархических функциональных связей между объектами системы. Эффективна на ранних стадиях создания системы, когда диаграммы просты и читаемы.

Методы проектирования, основанные на использовании структур данных, описаны ниже

j. Методология Джексона
Здесь структура данных - ключевой элемент в построении проекта. Структура программы определяется структурой данных, подлежащих обработке. Программа представляется как механизм, с помощью которого входные данные преобразуются и выходные. В методе предусматривается:

• разработка и изображение структуры входных и выходных данных;
• изображение структуры программы путем соединения изображений этих структурных элементов;
• определение дискретных операций над структурами данных;
• построение алгоритмов обработки структур данных.

k. Методология Уорнера
Подобна предыдущей, но процедура проектирования более детализована. Используются следующие виды представления проекта:

§ диаграммы организации данных (описывают входные и выходные данные)

§ диаграммы логического следования (логический поток этих данных);

§ список инструкций (команды, используемые в проекте);

§ псевдокод (описание проекта);

§ определение входных данных системы;

§ организация входных данных в иерархическую структуру;

§ детальное определение формата элементов входного файла;

§ то же самое для выходных данных;

§ спецификация программы: чтение, ветвление, вычисление, выходы, вызовы подпрограмм

§ составление диаграммы (по типу блок-схем) указывающие логическую последовательность инструкций.

l. Метод иерархических диаграмм
В этом методе определяется связь между входными, выходными данными и процессом обработки с помощью иерархической декомпозиции системы (без детализации). По сути используются три элемента: вход, обработка, выход. Алгоритм проектирования по этому методу заключается в следующих шагах:

§ начать с наивысшего уровня абстракции, определив вход, выход, обработку;

§ соединить каждый элемент входа и выхода с соответствующей обработкой;

§ документировать каждый элемент системы, используя диаграммы;

§ детализировать диаграммы, используя шаги 1-3.

m. Объектно-ориентированная методология проектирования
Основана на концепции упрятывания информации и абстрактных типов данных. Рассматриваются данные, модули и системы в качестве объектов. Каждый объект содержит некоторую структуру данных с набором процедур, знающих как работать с этими данными. По этой методологии создаются абстракции по заданной проблемной области:

• определение проблемы;
• развитие неформальной стратегии, удовлетворяющей требованиям к системе;
• формализация стратегии;
• создание объектов и их атрибутов;
• определение операций над объектами;
• установка интерфейсов;
• реализация операций.
1. построение модели;
   Построение модели в большинстве случаев является непростой задачей. Чтобы приобрести опыт в моделировании, необходимо изучить как можно больше известных и удачных моделей. При построении моделей, как правило, используют два принципа дедуктивный (от общего к частному) и индуктивный (от частного к общему).
   
   При дедуктивном подходе рассматривается частный случаи общеизвестной фундаментальной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Например, можно построить модель свободно падающего тела на основе известного закона mа = mg-F_сопр и в качестве допустимого приближения принять модель равноускоренного движения для малого промежутка времени.
   

Рис.12. Схема построения модели при индуктивном способе

Индуктивный способ (рис.12) предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, затем синтез. Здесь широко используется подобие, аналогичное моделирование, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы. Технология построения модели при индуктивном способе может быть представлена так:

0. эмпирический этап

• умозаключение
• интуиция
• предположение
• гипотеза
1. постановка задачи для моделирования
2. оценки; количественное и качественное описание
3. построение модели

4. разработка алгоритма
Разработка алгоритма - самый сложный и трудоемкий процесс, но и самый интересный в творческом отношении. Выбор метода разработки зависит от постановки модели. На этом этапе необходимо провести анализ правильности алгоритма, что очень непросто и трудоемко. Наиболее распространенная процедура доказательства - это прогон его на множестве различных тестов. Однако, это не гарантирует того, что не может существовать случая, в котором программа "не сработает", В общей методике доказательства правильности алгоритма предполагают, что алгоритм описан в виде последовательности шагов. Для каждого шага предполагается некое обоснование его правильности для всех подходящих входных(условиях данного шага) и выходных данных (условиях после этого шага). Затем предполагается доказательство конечности алгоритма с окончательными исходными входными и выходными данными

Алгоритм – это определенная последовательность инструкций (предписаний), доступные для понимания исполнителем и предназначенные для достижения им указанной цели или решения поставленной задачи.

Исполнитель алгоритма – это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.

В качестве исполнителя алгоритма могут выступать: человек, животное и автоматическое устройство. В информатике универсальным исполнителем алгоритмов является компьютер.

Исполнителя характеризуют:

· среда (или обстановка) – "место обитания" исполнителя;

· система команд – каждый исполнитель может выполнять команды только из некоторого строго заданного списка. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды;

· элементарные действия – то, что исполнитель совершает после вызова соответствующей команды;

· отказы – возникают, если команда вызывается при недопустимом для нее состоянии среды.

Обычно исполнитель ничего не знает о цели алгоритма. Он выполняет все полученные команды, не задавая вопросов "почему" и "зачем".

Изучение алгоритмов является спецификой науки о вычислениях. В последнее время здесь были достигнуты значительные успехи. К числу основных проблем, изучаемых этой наукой можно отнести следующие: поиск новых и улучшение существующих алгоритмов; математическое исследование эффективности алгоритмов; разработка математических методов доказательства того, что данный алгоритм является "наилучшими из возможных"; согласование положений теории вычислений с практическими соображениями.

К числу основных свойств алгоритма относятся следующие:

· Понятность (доступность) – алгоритм должен учитывать специфику исполнителя и, при необходимости, ему должны предоставляться дополнительные сведения;

· Дискретность (раздельность) – выполнение каждого очередного шага алгоритма должно начинаться только после полного завершения предыдущего шага;

· Детерминированность (определенность) – выполнение алгоритма исполнителем носит механический характер, т.е. выбор каждого очередного шага алгоритма зависит не от предпочтений исполнителя, а от результатов, достигнутых им на предыдущем шаге;

· Результативность (конечность) – либо решение задачи достигается за конечное, хотя бы и большое, число шагов, либо делается вывод о невозможности продолжения выполнения алгоритма по той или иной причине (есть алгоритмы, не обладающие этим свойством – например, вычисление иррационального числа p);

· Массовость – если алгоритм позволяет решить некоторую задачу, то он же должен быть применим для целого класса подобных задач, различающихся лишь наборами исходных данных, образующих область применимости алгоритма (есть алгоритмы, не обладающие этим свойством, т.к. порой невозможно организовать еще один набор исходных данных либо в силу их уникальности, либо в связи со значительными затратами времени, финансов или материальных ресурсов).

На практике используются следующие формы представления алгоритмов:

· Словесная запись (не формализованная запись алгоритма на естественном языке, например, рецепт приготовления манной каши);

· Блок-схема (наиболее наглядная графическая форма представления алгоритмов, используемая профессионалами особенно в тех случаях, когда алгоритм обладает изощренной логикой исполнения);

· Псевдокоды (язык программирования для бедных, когда нет возможности преподавать основы алгоритмизации с использованием ЭВМ – полуформализованные описания алгоритмов, включающий в себя как элементы "птичьего" языка программирования);

· Компьютерная программа (жестко формализованная запись алгоритма, ориентированная на исполнителя – ЭВМ). Для разработки компьютерных программ используются инструментальные средства, называемые языками программирования.

Рассмотрим запись алгоритма Евклида нахождения наибольшего общего делителя (НОД) для двух натуральных чисел во всех четырех перечисленных выше формах.

		проверка условия Это линейный тип алгоритма (следование)
		к содержанию задание исходных данных, вывод результата

Словесная запись:

1. Задать два числа.

2. Если числа равны, то взять первое из них в качестве ответа и прекратить выполнение алгоритма, иначе идти к пункту 3.

3. Определить бóльшее из двух чисел.

4. Заменить бóльшее число на разность между бóльшим и меньшим числами.

5. Идти к пункту 2.

Блок-схема:

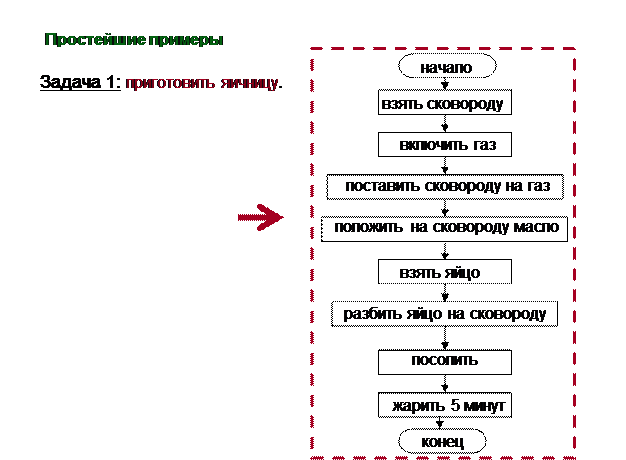
Псевдокоды:

алг НОД

нач

ввод a; b

S: если a < > b тоидти к F

если a < b то a:=a-b

иначе b:=b-a

идти к S

F: вывод a

Дата добавления: 2014-01-20