Двоично-десятичные системы счисления

Помимо естественных систем следует различать еще весомозначные смешанные системы. В общем случае, веса в смешанной системе определяются матрицей

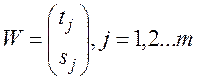, (3.3)

где 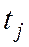- число разрядов в j-й группе последних; 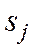- натуральные основания естественной системы, в которой записываются цифры j-й группы.

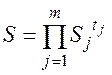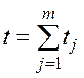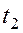
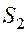При этом предполагается, что влево от выделенной совокупности групп разрядов имеет место та же совокупность групп с теми же однозначно сопоставленными им основаниями, т.е. последней совокупности групп также отвечает матрица вида (3.3). Такую систему можно рассматривать как естественную систему с натуральным основанием , в которой каждый разряд кодируется совокупностью из разрядов (-ичных, -ичных, …,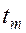 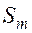-ичных).

Наибольший интерес для нас представляют смешанные системы, в которых каждый разряд обычной десятичной системы заменяется четырьмя двоичными разрядами. Такие системы называют двоично-десятичными, а четверки двоичных разрядов, используемые для кодирования десятичных цифр, – тетрадами. Причем двоично-десятичное кодирование, как это будет рассмотрено далее, следует рассматривать как дальнейшее развитие введенного выше понятия смешанной системы.

Общее число различных способов двоично-десятичного кодирования, включая абсолютно бессмысленные, равно, как легко понять, 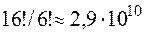. Однако далеко не все из них можно рекомендовать для практического использования. Типичными требованиями, предъявляемыми к двоично-десятичной системе при её применении в ЭВМ, являются требования Рутисхаузера, заключающиеся в следующем:

1. Требование единственности. Каждой десятичной цифре должна взаимно однозначно соответствовать некоторая двоичная тетрада.

2. Требование весомозначности. Должна существовать такая четверка целых чисел 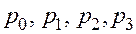, называемых весами, что если десятичная цифра имеет код 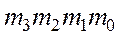, то .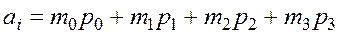

3. Требование дополнительности. Если десятичные цифры 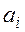и 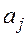таковы, что , то, если цифре 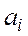отвечает код 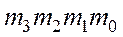, то цифра 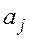должна кодироваться тетрадой 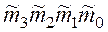, где

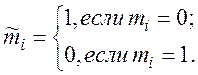
4. Требование упорядоченности. Бóльшим десятичным цифрам должны соответствовать бóльшие тетрады (возможно выполнение противоположного требования).

5. Требование четности. Четные и нечетные десятичные цифры должны кодироваться четными и нечетными тетрадами соответственно (возможна реализация противоположного требования). При этом тетрада считается четной, если .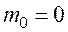

Удовлетворение этим требованиям позволяет говорить о практическом использовании в ЭВМ соответствующей двоично-десятичной системы и эффективном кодировании (1-е требование), облегчает логику операций в ней и процесс перехода к десятичному кодированию (2-е требование), упрощает выполнение операции двоично-десятичного алгебраического сложения (3-е требование), дает возможность легко реализовать двоично-десятичное сравнение кодов (4-е требование), открывает путь к простым алгоритмам округления данных при их двоично-десятичном представлении, а также к несложным алгоритмам деления, извлечения корня и некоторых логических операций (5-е требование).

Существуют только две двоично-десятичных системы, удовлетворяющие всем требованиям [3.1 ]. Это системы с весами 4,2,2,1 и 2,4,2,1, называемые еще кодами Эмери (см. табл.3.9). Один из них (код 2,4,2,1) был впервые использован в одной из швейцарских ЭВМ, а затем получил достаточно широкое распространение.

Иногда к двоично-десятичным системам предъявляют другие требования. Одним из них является требование однозначности представления, которое следует отличать от первого требования Рутисхаузера. Считают, что система удовлетворяет требованию однозначности представления, если каждой десятичной цифре в ней отвечает при выбранных весах только одна из 16 тетрад. Код 2,4,2,1 не удовлетворяет этому требованию, поскольку цифра 2 в нем может быть представлена как 1000 и как 0010.

Показано, что при положительных весах единственной двоично-десятичной системой, удовлетворяющей требованию однозначности, является система с весами 8,4,2,1. При наличии отрицательных весов таких систем насчитывается 21. Таким образом, если учесть, что при потетрадном кодировании весомозначные двоично-десятичные системы не могут иметь дробных весов, то общее число систем, отвечающих требованию однозначности, равно 22.

Существуют также двоично-десятичные системы, не являющиеся весомозначными, весьма просто связанные с какой-либо весомозначной системой того же типа, обеспечивая при этом простоту выполнения арифметических операций. Среди них наиболее известны системы с избытком относительно систем с весами 8,4,2,1. Эти системы получаются из кода прямого замещения прибавлением к каждой тетраде некоторого постоянного числа, называемого избытком. Последний может составлять от 1 до 15.

Легко убедиться, что все такие системы, начиная с системы, имеющий избыток 7, не удовлетворяют требованию упорядоченности. Системы с избытками, меньшими 7, отвечают 1, 4 и 5 требованиям Рутисхаузера, и лишь одна из них, имеющая избыток 3, удовлетворяет еще и требованию дополнительности (см. табл. 3.9).

Рассмотрим подробнее некоторые двоично-десятичные системы. Наибольший интерес среди них представляют коды Эмери, код прямого замещения и код с избытком 3.

3.9

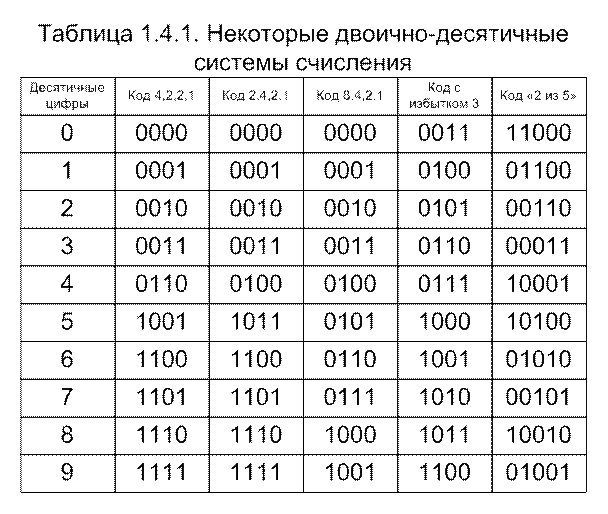
Коды 4,2,2,1 и 2,4,2,1 удовлетворяют всем требованиям, код 8,4,2,1 не удовлетворяет требованию дополнительности, а код с избытком 3 – требованию весомозначности. Используя правила выполнения арифметических действий в двоичной и десятичной системах, а также свойства рассматриваемых кодов, можно сформулировать алгоритмы сложения, вычитания, умножения и деления многоразрядных чисел в этих кодах, пригодные в большей или меньшей степени и для реализации в ЭВМ. Однако отсутствие дополнительности кода 8,4,2,1 настолько усложняет алгоритм вычитания, а следовательно и деления в нем, что применение его в качестве основного машинного кода имеет место в исключительных случаях. Вместе с тем, этот код используется в качестве служебного кода практически во всех ЭВМ, работающих в канонической двоичной системе счисления. Это связано с легкостью визуального и машинного перевода десятичных чисел в код прямого замещения и обратно (см. раздел 1.2). Поскольку же для восприятия десятичных чисел такой машиной все равно необходимо какое-либо двоично-десятичное кодирование, то для этого целесообразно взять код 8,4,2,1.

В заключение следует отметить, что иногда для кодирования десятичных цифр используется избыточное число двоичных разрядов, что позволяет снизить расход потребляемой мощности. Если об этом судить по числу единиц, используемых в двоичных эквивалентах, то например, код 8,4,2,1 выгодней, чем код 2,4,2,1, или код с избытком 3, поскольку в нем на каждый десятичный разряд расходуется в среднем 1,5 двоичных единицы, а в коде 2,4,2,1 и с избытком 3 – по две. Если же каждую десятичную цифру закодировать восьмиразрядным двоичным эквивалентом (октадой), то этот показатель можно снизить до величины, меньшей 1.

Более существенным при избыточном кодировании является повышение его помехоустойчивости, которое, как правило, имеет место. Так, к примеру, в коде «2 из 5» (см. табл. 3.9) легко обнаруживается любая одиночная ошибка. Специальным кодированием можно добиться, что ошибки, в том числе и многократные, могут не только легко обнаруживаться, но и исправляться, причем не только при хранении или передаче информации, но и при выполнении арифметических операций. Однако выполнение последних при таком кодировании, как правило, ведет к очень сложным процедурам. Кроме того, для контроля правильности выполнения арифметических операций часто наиболее целесообразно использовать так называемый контроль по модулю. Поэтому применение для кодирования десятичных цифр избыточного числа двоичных разрядов имеет место, в основном, для целей контроля операций, связанных с передачей и хранением данных в ЭВМ.

Дата добавления: 2014-01-20