Перевод чисел из системы счисления с натуральным основанием в двоично-десятичную систему и обратно

По вполне понятным причинам наибольший интерес для нас представляют случаи, когда натуральное основание равно 10 или 2.

Перевод чисел из десятичной системы счисления в двоично-десятичную и обратно приходится выполнять практически в любой ЭВМ, использующей двоично-десятичную систему в качестве служебной или основной. Этот перевод реализуется чрезвычайно просто: для перевода кода 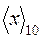в код необходимо каждую десятичную цифру заменить двоичной тетрадой в соответствии с выбранной системой кодирования; при обратном переходе двоично-десятичная запись разбивается на тетрады влево и вправо от запятой, каждая из которых замещается затем отвечающей ей десятичной цифрой.

Перевод же чисел из двоичной системы счисления в двоично-десятичную и обратно имеет место всякий раз, когда в ЭВМ в качестве основной системы используется двоичная. При этом, как правило, двоично-десятичная система является служебной и, как отмечалось в подразделе 3.1.4, для этих целей наиболее целесообразно использовать код прямого замещения. Рассмотрим вопросы перевода кода 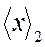в код 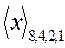и обратно несколько подробнее.

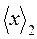
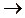
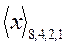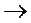
Существует несколько алгоритмов преобразования и , базирующихся на правилах перевода, изложенных в подразделе 3.2.1. Одни из них предпочтительнее при схемной, а другие – при программной реализации. К первой группе относятся, например, алгоритмы, изложенные в [3.1]. Характерной для некоторых из них является ориентация на двоично-десятичные блоки в составе преобразователей, что в рассматриваемом нами случае представляет ограниченный интерес. Однако, незначительная модернизация последних алгоритмов позволяет реализовать и их на базе устройств, работающих в двоичной системе счисления.

3.2.2.1. Пусть первоначально 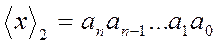. Тогда преобразование наиболее часто выполняется с помощью соотношения

.

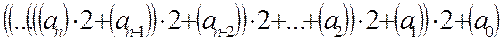При этом можно воспользоваться обычным двоичным суммирующим устройством.

Разобьем разрядную сетку последнего влево от запятой на группы по четыре двоичных разряда в группе. В младший разряд младшей группы в каждом цикле преобразования будем помещать цифры , начиная со старшей. Цикл преобразования состоит из такта сдвига содержимого суммирующего устройства на один разряд влево и такта его коррекции с целью восстановления истинных значений тетрад. Коррекция сводится к прибавлению к i-й тетраде кода , если ее значение после сдвига 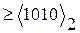или если в младший разряд (i+1)-й тетрады в процессе сдвига была занесена 1 из старшего разряда i-й тетрады (занесение очередной цифры 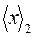в младший разряд младшей тетрады не относится к этому случаю). При этом суммирование проводится с учетом межтетрадных переносов. Общее число циклов преобразования равно n+1.

Рассмотрим пример преобразования =1001011.

Имеем

Результат преобразования 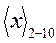= 0111 0101. Квадратными скобками отмечены последовательно анализируемые разряды .

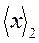3.2.2.2. Пусть теперь . В этом случае для преобразования используется процедура

.

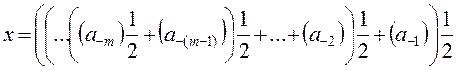Разрядная сетка двоичного суммирующего устройства разбивается здесь на группы вправо от запятой; занесение цифр 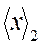, начиная с младшей, производится в каждом цикле преобразования в старший разряд старшей тетрады; содержание суммирующего устройства сдвигается в такте сдвига на один разряд вправо. По-другому выполняется и коррекция. Она сводится к прибавлению к младшей тетраде 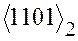, если в старший ее разряд в процессе сдвига заносится из младшего разряда старшей тетрады 1 (сюда же относится и случай занесения очередной цифры 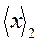в старший разряд старшей тетрады). При этом в процессе суммирования межтетрадные переносы игнорируются. Общее число циклов преобразования равно m.

Пусть, к примеру, =0,1010001.

Тогда имеем

Результат преобразования, полученный с точностью 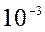, 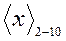=0,0110 0011 0010 (квадратными скобками отмечены последовательно анализируемые разряды ).

Конечно, для игнорирования межтетрадных переносов необходимо принимать специальные меры, что неудобно. Однако при желании это неудобство легко устраняется следующим образом. В каждом цикле преобразования будем первоначально прибавлять к каждой младшей тетраде код , если в младшем разряде старшей тетрады находится 1 (роль этого разряда для самой старшей тетрады играет очередной 0. разряд). Одновременно с этим упомянутая 1 заменяется Межтетрадные переносы в процессе суммирования не блокируются. Далее обычным порядком производится сдвиг содержимого суммирующего устройства на один разряд вправо, и цикл преобразования заканчивается.

3.2.2.3. Положим далее, что задано в коде прямого замещения число 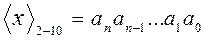. Преобразование можно осуществить по описанному в подразделе 3.2.1 методу деления. Для этого достаточно поместить 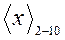на двоичное суммирующее устройство и выполнить операции, описанные в п.3.2.2.2, с той лишь разницей, что в рассматриваемом случае никаких занесений в старший разряд старшей тетрады не происходит. Цифры , начиная с младшей, получаются в процессе сдвига на выходе младшего разряда младшей тетрады. Проиллюстрируем сказанное на примере, полагая, что используется модификация алгоритма, при которой межтетрадные связи во время коррекции не блокируются. Число циклов преобразования равно .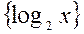

Пусть 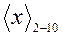=0111 0101. Имеем

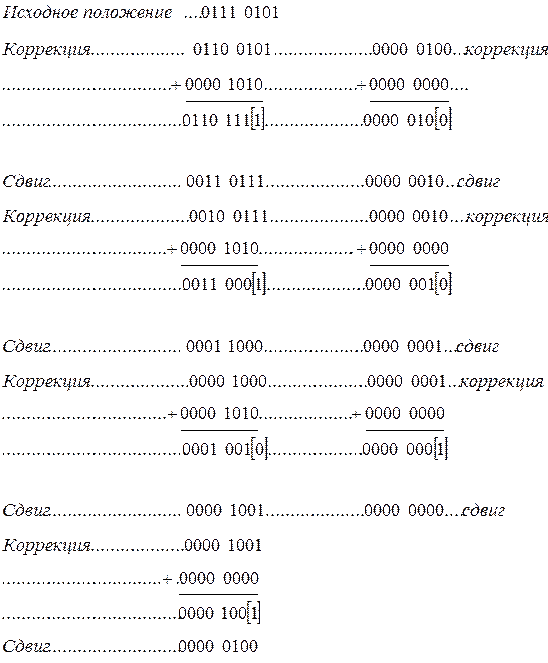
Последовательно получаемые цифры 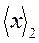заключены в квадратные скобки. Как видим, 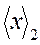=1001011.

В работе [3. 1] приведен алгоритм преобразования целых кодов 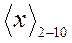в соответствующие им коды 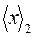, базирующийся на методе непосредствнной замены.

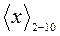
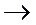
3.2.2.4. Рассмотрим, наконец, преобразование 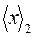, когда 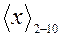является дробным. Используем для этих целей метод умножения. Поместим на двоичное суммирующее устройство и выполним операции, описанные в п.3.2.2.1, с той лишь разницей, что при появлении в такте сдвига в разряде целых 1 к старшей тетраде в такте коррекции также будем прибавлять . Цифры 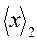фиксируются в разряде целых по окончании цикла преобразования. Общее число этих циклов определяется требуемой точностью перевода. Проиллюстрируем сказанное примером.

Пусть 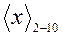=0,0111 0011. Получим

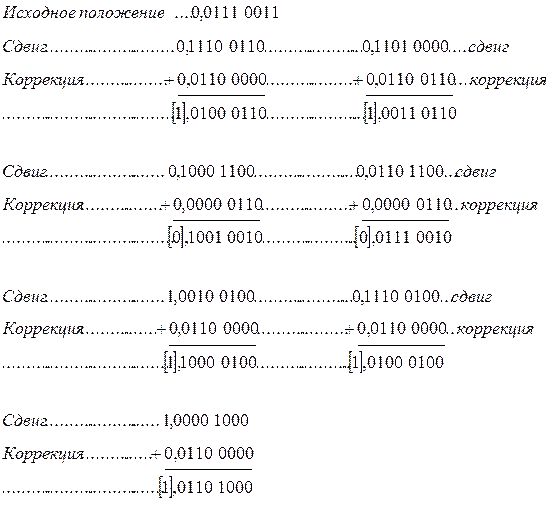
Последовательно получаемые цифры заключены в квадратные скобки. Как видим, 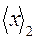=0,1011101 с точностью .

В работе [3. 1] изложены и другие подходы к переводу 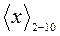и обратно, в том числе и для других способов кодирования десятичных цифр двоичными тетрадами. Алгоритмы такого перевода (при использовании кода прямого замещения), удобные для программной реализации, приведены в [3.1 ].

Дата добавления: 2014-01-20