Расчет надежности электрических сетей методом случайных процессов

Если интенсивность отказов элементов постоянна в течение года, а время восстановления и появления отказов определяются экспоненциальным законом распределения, то случайный процесс аварий и восстановлений можно описать цепями Маркова.

Пусть нам известны вероятности перехода из рабочего состояния в состояние отказа 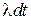и обратно в течение промежутка времени , настолько малым, чтобы найти границу во времени между различными состояниями элемента.

Распределение времени появления отказов

,

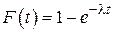условная вероятность отказа в интервале (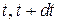) равна 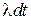. Здесь - интенсивность отказов.

Распределение времени ремонта

,

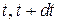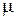условная вероятность завершения ремонта в интервале () - . Здесь - интенсивность восстановления (ремонта).

Марковский процесс полностью определен, если заданы все условные (переходные) вероятности перехода из (S - 1)-гo в S –е состояние и начальное состояние системы. Максимальное число состояний системы 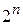, 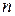- число элементов.

Для вычисления вероятностей перехода составляют диаграмму переходов системы (рис. 14). Индекс «0» означает рабочее состояние; «1» - отказ. Для диаграммы переходов составляют матрицу вероятностей перехода.

Диагональ матрицы показывает вероятности сохранения рабочего или ремонтного состояния. Остальные элементы - вероятности перехода из j- го состояния в i -е.

Рис. 14. Диаграмма переходов для одного элемента

На основании матрицы вероятностей переходов получим:

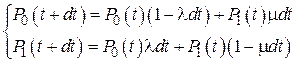
Взяв пределы

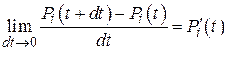
получим систему линейных дифференциальных уравнений с постоянными коэффициентами:

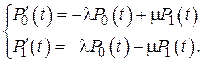
Если система при 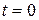исправна, то начальные условия будут иметь вид

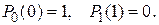
Если система при 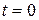находится в ремонте, то Интегрированием уравнений получают их общее решение

,

где 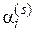- постоянные; 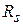- корни характеристического уравнения; 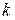- число состояний.

При 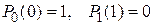получим (рис. 15):

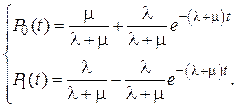
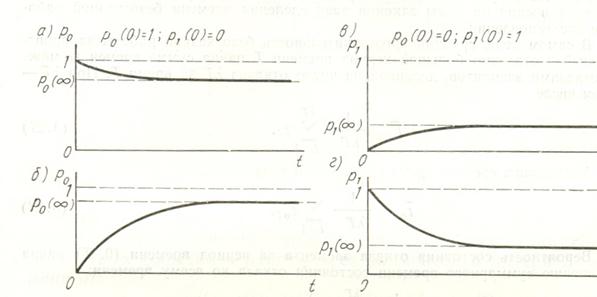
Рис. 15. Вероятности состояний для одного элемента

Решение системы дифференциальных уравнений требует вычисления определителя 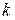-го порядка для составления характеристического уравнения; нахождения всех корней характеристического уравнения 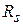(s = 1,2,...,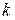); вычисления постоянных 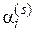путем решения 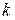+1 раз системы 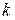линейных алгебраических уравнений.

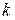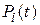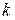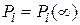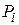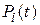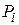Решение задачи возможно при несколько сотен. определяют при небольшом . Проще определить установившиеся вероятности состояния системы . Значения можно получить по выражениям , принимая . Можно определить , преобразовав систему дифференциальных уравнений, в которых , а .

(1)

К системе (1) добавляют уравнение

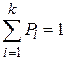(2)

Решая: совместно (2) с любым уравнением из системы (1), получим

.

Для расчета надежности сложной системы также составляют диаграмму переходов (рис. 16).

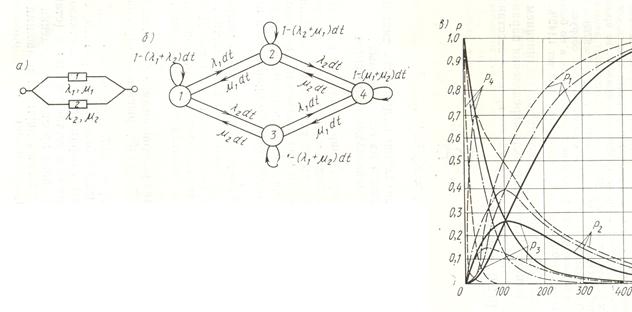
Рис. 16. Диаграмма переходов для системы из двух элементов

Некоторые состояния этой диаграммы могут соответствовать частичному ограничению потребителей. Вероятность таких ограничений можно определить, пользуясь матрицей вероятностей перехода.

.

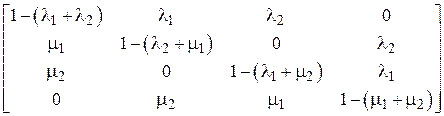При сложной схеме электрических сетей необходимо для каждого состояния системы выполнять расчеты потокораспределений. По результатам этих расчетов определяют дефициты мощности и энергии в узлах, их длительность и другие показатели надежности.

Дата добавления: 2014-01-20