
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие правила простого категорического силлогизма
|
|
|
|
I О
А Е

Рис. 32
3) Противопоставление предикату - это логическое действие, уточняющее смысл суждения посредством установления отношения не-Р к S. Все студенты (S)- учащиеся (Р) → Ни один не учащийся (не-Р) не является студентом (S). Мы сначала выполняем превращение исходного суждения, а затем его обращение. В результате получаем противопоставление предикату. А: Все лжецы - безнравственны. Превращение → Ни один лжец не является нравственным. Обращение → Ни один нравственный человек - не лжец.
Схема:
А: Все S суть Р → Е: ни одно ┐Р не есть S.
Е: Ни одно S не есть Р → I: Некоторые ┐Р суть S.
О: Некоторые S не суть Р → I: Некоторые ┐Р суть S.
А Е

I O
Рис. 33
Суждение типа «I» нельзя подвергнуть противопоставлению предикату, т.к. при превращении суждения I мы получим суждение типа «О», а оно, как мы видели, не подвергается обращению.
На основе логического квадрата можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения.
4) Умозаключения по логическому квадрату (рис. 34).
Здесь возможны следующие случаи:
А) выводы на основании отношения подчинения;
Б) выводы на основании отношения частичной совместимости;
В) выводы на основании отношения противоречия;
Г) выводы на основании отношения противоположности.
А) выводы на основании отношения подчинения:
 |
Рис. 34
А) выводы на основании отношения подчинения:
а) умозаключения от истинности одного к истинности другого и б) от ложности одного к ложности другого.
а) Умозаключения от истинности одного к истинности другого. Это умозаключения от А к I и от Е к О. Вид: А├ I, Е├ О, где ├ - знак логического следования. А: Все люди подвержены заблуждениям. ├ I: Некоторые люди подвержены заблуждениям. Е: Ни один человек не является непогрешимым ├ О: Некоторые люди не являются непогрешимыми.
б) Умозаключения от ложности одного к ложности другого. От ложности I к ложности А и от ложности О к ложности Е. Вид: ┐I├ ┐А, ┐О├ ┐Е. Из ложности суждения «Некоторые люди способны летать» следует ложность суждения «Все люди способны летать». Из ложности суждения «Некоторые люди есть птицы» следует ложность суждения «Все люди есть птицы».
Б) Выводы на основании отношения частичной совместимости.
Это отношение - между суждениями I и О. Здесь возможны только выводы от ложности к истинности, т.к. эти суждения не могут быть вместе ложными, но могут быть вместе истинными. ┐I├ О, ┐О ├ I. В силу тривиальности используются редко.
В) Выводы на основании отношения противоречия:
а) от ложности некоторого суждения к истинности другого. ┐А├ О, ┐О ├ А, ┐Е├ I, ┐ I ├ Е. Из ложности суждения «Все люди - преступники» следует истинность суждения «Некоторые люди - не преступники.» Из ложности суждения «Некоторые зайцы - птицы» следует истинность суждения «Ни один заяц не есть птица».
б) от истинности некоторого суждения к ложности другого. А├ ┐О, О ├ ┐А, Е├ ┐I, I ├ ┐Е.
Из истинности суждения «Ни один лентяй не заслуживает похвалы» следует ложность суждения «Некоторые лентяи заслуживают похвалы».
Г) выводы на основании отношения противоположности.
Здесь возможны выводы только от истинности к ложности, т.к. суждения, находящиеся в отношении противоположности, не могут быть вместе истинными, но могут быть вместе ложными. А ├ ┐Е, Е ├ ┐А. Из истинности суждения «Все студенты - учащиеся ВУЗов» следует ложность суждения «Ни один студент не является учащимся ВУЗа».
Опосредованные умозаключения. Силлогизмы.
Опосредованные умозаключения состоят из нескольких (двух и более посылок). Они подразделяются на:
1) Опосредованные умозаключения из простых суждений
2) Опосредованные умозаключения из сложных суждений
Опосредованные умозаключения из простых суждений подразделяются на умозаключения из атрибутивных (категорических) суждений и умозаключения из суждений об отношениях (реляционных).
К свойствам умозаключений с отношениями (вида аRв) относятся:
1. Симметричность (если а=в, то в=а);
2. Асимметричность (если а больше в, то в меньше а);
3. Переходность (транзитивность) (если а больше в, в больше с, то а больше с). Пример. Если 8 больше 3, а 3 больше 2, то 8 больше 2.
Силлогизм - форма дедуктивного умозаключения, в которой из суждений с субъектно-предикатной формой выводится новое суждение. В силлогизме предпосылками являются атрибутивные суждения.
Силлогистику (логическую теорию дедуктивного рассуждения) создал Аристотель. Она устанавливает условия, при которых из одного или нескольких истинных суждений с необходимостью следует истинное заключение, а также условия, при которых такое следование невозможно.
Простой категорический силлогизм (ПКС) - это дедуктивное умозаключение, в котором из двух простых категорических суждений, связанных общим средним термином, выводится новое простое категорическое суждение.
Пример: Все люди (М) смертны (Р). Все греки (S) - люди (М). ├ Все греки (S) смертны (Р).

Рис. 35
В ПКС - три термина:
1. М - общий термин, входящий в обе посылки и не входящий в заключение.
2. Р - больший термин, являющийся предикатом заключения.
3. S - меньший термин, являющийся субъектов заключения.
В ПКС одна из предпосылок - обязательно общее суждение. Суждения, содержащие средний термин, являются посылками. Посылка, содержащая предикат заключения (больший термин Р) - большая посылка. Посылка, содержащая субъект заключения (меньший термин S) - меньшая посылка.
Приведенный в данном примере ПКС может быть записан следующим образом:
Все М суть Р
Все S есть М
___________
Все S есть М
Здесь: Все М суть Р - большая посылка; Все S есть М - меньшая посылка; Все S есть М - заключение.
Аксиома силлогизма: Все, что утверждается относительно всего множества, утверждается и относительно каждого его подмножества, и все, что отрицается относительно всего множества, отрицается и относительно каждого его подмножества.
Признак признака вещи есть признак самой вещи, а то, что отрицается относительно признака вещи, отрицается и относительно самой вещи.
В ПКС могут быть выделены его содержание и форма. Содержание силлогизма - это понятия, встречающиеся в нем в качестве терминов. Форма силлогизма - это связь, которая придается терминам.
Мы можем выделить форму силлогизма о греках:
Все М есть Р.
Все S есть М.
__________
Все S есть Р
Правила терминов:
1. В силлогизме должны быть только три термина, т.е. М - средний термин - должен быть тождествен, иметь один смысл.
2. Средний термин должен быть распределен хотя бы в одной посылке. Если он не распределен - вывод будет неопределенным.
Пример:
Все художники (Р) тонко чувствую природу (М).
Петров (S) тонко чувствует природу (М).
Следовательно, Петров (S) - художник (Р).
Причина неопределенности в том, что средний термин (М), занимающий место предиката и в большей и в меньшей посылках - не распределен (обе они - утвердительные, а в них, как правило, предикат не является распределенным.
3. Термин, не распределенный в посылках, не может быть распределен и в заключении (из мысли о части нельзя вывести мысль о целом).
Пример:
Все учебники (М) - полезны (Р),
Все учебники (М) - книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Мы не можем сказать «все книги полезны». Суть в том, что «книги» - предикат в меньшей посылке, которая есть утвердительное суждение с нераспределенным предикатом.
Правила посылок.
1. Хотя бы одна посылка должна быть утвердительным суждением.
Пример.
Стекло (М) не электропроводно (Р).
Дерево (S) - не стекло (М).
Следовательно, дерево (S) - электропроводно (Р).
Вывод или ложный или неопределенный.
2. Если одна посылка - отрицательное суждение, то заключение - отрицательное.
Пример.
Всякое преступление (Р) есть правонарушение (М).
Моральный поступок (S) не есть правонарушение (М).
Следовательно, моральный поступок (S) не есть преступление (Р).
3. Хотя бы одна посылка должна быть общим суждением.
Некоторые депутаты (М) - ученые (Р).
Некоторые артисты (S) - депутаты (М).
Следовательно, некоторые артисты (S) - ученые (Р). А может быть, все или ни один?
4. Если одна посылка - частное суждение, то и заключение - частное суждение. Если одна из посылок - частное суждение, то и вывод - частный.
Пример.
Некоторые пенсионеры (Р) - работающие (М)
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) - пенсионеры (Р).
Фигуры и модусы силлогизма.
В ПКС различают фигуры и модусы. Фигуры силлогизма - это его разновидности, различающиеся положением среднего термина в посылках (рис. 36). Модусы силлогизма - это его разновидности, различающиеся определенным сочетанием количества и качества составляющих его суждений - общеутвердительных, частноутвердительных, общеотрицательных, частноотрицательных). (ААА, ЕАЕ….). Каждой фигуре соответствует определенный набор модусов.
Фигура 1 - наиболее распространена. Суть ее - подведение частного случая под общий.
Два правила первой фигуры:
1. Большая посылка - общее суждение.
2. Меньшая посылка - утвердительное суждение.
Пример.
Всякое преступление (М) есть правонарушение (Р).
Кража (S) есть преступление (М).
Следовательно, кража (S) есть правонарушение (М).
Модусы первой фигуры: ААА, ЕАЕ, АII, EIO.
М Р Р М
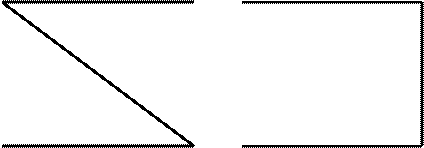
S M S M
Фигура 1 Фигура 2
М Р Р М
 |  |
М S М S
Фигура 3 Фигура 4
Рис. 36
Фигура 2 - показывает, что частный случай нельзя подвести под общий. «Что противоречит признаку вещи, противоречит самой вещи».
Два правила второй фигуры:
1. Большая предпосылка - общее суждение.
2. Одна из посылок - отрицательное суждение.
Пример.
Все юристы (Р) знают логику (М).
П. (S) не знает логики (М).
Следовательно, П. (S) - не юрист (Р).
Модусы второй фигуры: ЕАЕ, АЕЕ, ЕИО, АОО.
Фигура 3. Суть третьей фигуры в том, что она, давая частные заключения, устанавливает частичную совместимость
Два правила третьей фигуры:
1. Меньшая посылка - утвердительное суждение.
2. Заключение - частное суждение.
Пример.
Все философы (М) стремятся к истине (Р).
Некоторые философы (М) ищут успеха у женщин (S).
_____________________________________________
Некоторые из тех, кто ищет успеха у женщин (S) стремятся к истине (Р).
Модусы третьей фигуры: AAI, IAI, AII, EAO, OAO, EIO.
Фигура 4. Ход рассуждений по 4 фигуре ПКС нетипичен для процесса мышления, а познавательная ценность заключения - невелика, поэтому ее применение в логической практике весьма ограничено.
Пример.
Ни один счастливый человек (Р) не стремится к справедливости (М).
Некоторые стремящиеся (М) к справедливости - юристы (S).
____________________________________________________
Некоторые юристы (S) не являются счастливыми людьми (Р).
Разделительное умозаключение и его разновидности.
1) Разделительно-категорический силлогизм – это умозаключение, в котором одна посылка – разделительное (дизъюнктивное) суждение, а другая посылка и заключение – категорические суждения. Разделительно-категорический силлогизм также имеет свои модусы:
 1) Утверждающе-отрицающий модус (modus ponendo tollens)
1) Утверждающе-отрицающий модус (modus ponendo tollens)
<p ۷ q ۷ r>, p
 ┐q ^ ┐r
┐q ^ ┐r
Здесь меньшая посылка – категорическое суждение – утверждает одну из альтернатив, а заключение отрицает все остальные альтернативы. Дизъюнкция должна быть обязательно строгая.
Пример.
Вывод может быть либо утвердительным (р), либо отрицательным (q), либо неопределенным (r).
Полученный вывод является утвердительным (р).
_________
Полученный вывод не является ни отрицательным (┐q), ни неопределенным (┐r).
2) Отрицающе-утверждающий модус (modus tollendo ponens)
< p ۷ q >, ┐p
 q
q
Здесь меньшая посылка – категорическое суждение – отрицает все альтернативы, кроме одной, а заключение утверждает оставшуюся альтернативу.
Пример.
Люди либо содействуют (р) либо противодействуют (q) ходу истории.
М. не содействовал (┐p) ходу истории.
_________
М. противодействовал (q) ходу истории.
Условно-разделительный силлогизм – это умозаключение, в котором большая посылка состоит из двух и более условных суждений; а меньшая посылка – разделительное суждение. Еще его называют лемматическое умозаключение (lemmа – лат. предположение). При двух альтернативах получается дилемма, при трех – трилемма.
Рассмотрим виды дилемм:
1) Простая конструктивная дилемма. Формула имеет вид:
 (p → r) ۸ (q → r), p۷q
(p → r) ۸ (q → r), p۷q
r
В простой конструктивной дилемме условная посылка содержит два основания, из которых вытекает одно и то же следствие. Разделительная посылка утверждает оба возможных основания. Заключение утверждает следствие. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствия.
Пример.
Если Госбанк будет увеличивать денежную эмиссию (р), то инфляция возрастет (r).
Если Госбанк будет давать нерентабельным предприятиям льготные кредиты (q), то инфляция возрастет (r).
Но Госбанк или занимается эмиссией денег, или дает льготные кредиты нерентабельным предприятиям.
_____________________________
Следовательно, нам не избежать инфляции (r).
2) Сложная конструктивная дилемма. Формула имеет вид:
(p → q) ۸ (r → s), p۷r
 q۷s
q۷s
В сложной деструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка утверждает оба возможных основания. Заключение утверждает оба возможных следствия. Рассуждение направлено от утверждения истинности оснований к утверждению истинности следствий.
3) Простая деструктивная дилемма. Формула имеет вид:
 (p → q) ۸ (p → r), ┐q۷ ┐r
(p → q) ۸ (p → r), ┐q۷ ┐r
┐p
В простой деструктивной дилемме условная посылка содержит одон основание, из которого вытекают два возможных следствия. Разделительная посылка отрицает оба следствия. Заключение отрицает основание. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности основания.
Пример.
Если хочешь быть счастливым (р) в наше время, нужно иметь много денег (q).
Однако во все времена было: если хочешь быть счастливым (р), нужно иметь чистую совесть (r).
Но одновременно невозможно иметь много денег и совесть, т.е. или нет денег (┐q), или нет совести (┐r).
_______________________________
Следовательно, оставь надежду на счастье (┐р).
4) Сложная деструктивная дилемма. Формула имеет вид:
 (p → q) ۸ (r → s), ┐q۷┐s
(p → q) ۸ (r → s), ┐q۷┐s
┐p۷┐r
В сложной деструктивной дилемме условная посылка содержит два основания и два следствия. Разделительная посылка отрицает оба следствия. Заключение отрицает оба основания. Рассуждение направлено от отрицания истинности следствий к отрицанию истинности оснований.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1249; Нарушение авторских прав?; Мы поможем в написании вашей работы!