Симплекс-метод. При решении ЗЛП симплекс-методом удобно представить задачу в табличном виде

При решении ЗЛП симплекс-методом удобно представить задачу в табличном виде.

№	б.п.	х1	...	хj*	...	xn	b
	xa1	a11	...	a1j*	...	a1n	b1
...	...	...	...	...	...	...
xai*	ai*1	...	ai*j*	...	ai*n	bi*
...	...	...	...	...	...	...
xam	am1	...	amj*	...	amn	bm
F(x)	C1	...	Cj*	...	Cn	F0

ПРИЗНАК ОПТИМАЛЬНОСТИ. План х* = (х₁, х₂,..., х_n) считается оптимальным, если все коэффициенты целевой функции неотрицательны, С_j ³ 0,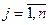. Тогда значение F_max равно значению, стоящему в правом нижнем углу таблицы.

Если имеется хотя бы один отрицательный коэффициент целевой функции, следует перейти к новому базисному решению, значение целевой функции при котором будет меньше. Для этого используют следующие правила:

1) Среди отрицательных коэффициентов целевой функции выбирают максимальный по модулю. Столбец, в котором стоит этот коэффициент, называют разрешающим и помечают *.

2) Находят отношения 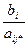, т.е. отношения свободных членов ограничений к элементам матрицы коэффициентов ограничений, стоящим в разрешающем столбце и имеющим положительные значения. Среди этих отношений выбирают минимальное. Строка, в которой стоит это минимальное отношение, называется разрешающий и помечается *. Если среди элементов разрешающего столбца не будет ни одного положительного, то задача оптимизации не имеет решения.

3) Элемент, стоящий на пересечении разрешающих строки и столбца, называется разрешающим и отмечается .

4) Производится замена базисного допустимого решения на другое, при этом таблица будет иметь следующее содержание:

а) свободная переменная х_j*, стоящая в разрешающем столбце, становится базисной, а

базисная переменная х_ai*, стоящая в разрешающей строке, - свободной;

б) все элементы разрешающей строки в новой таблице имеют значения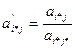

(штрихом отмечены новые значения);

в) все остальные элементы таблицы определяются по формулам:

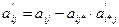(i¹i*), 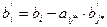(i¹i*),

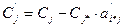(i¹i*), .

Каждая новая таблица проверяется на оптимальность. Операции 1)-4) осуществляются до тех пор, пока не будет получено оптимальное значение целевой функции.

Дата добавления: 2014-01-20