Теория полезности

Теория принятия решений.

Модели принятия решения.

Модели научения.

Вероятностные модели представляют самый широкий класс моделей в психологии. Модели такого типа существуют почти во всех её разделах. Далее будут приведены лишь отдельные, наиболее характерные примеры.

Так, в моделях научения есть класс вероятностных моделей. Примером общей вероятностной модели процесса научения является модель, имеющая два подмножества гипотез. (K.Chow, J.Cotton, 1983; Ch.Brainerd, 1982). Согласно этим моделям, испытуемый выдвигает гипотезу из одного подмножества; в случае верного решения в следующем испытании гипотеза выдвигается из этого же множества, а в случае неудачи – с вероятностью p происходит выбор одного из двух подмножеств. Однако модели, имеющие три подмножества гипотез, более адекватно отражают процесс идентификации понятий.

В качестве примера адекватной вероятностной модели можно привести разработанную А.Дрынковым (1985) модель, описывающие кривые научения и представляющую собой автомат-подкрепление со счётным множеством расстояний.

Теория принятия решений представляет собой набор понятий и семантических методов, позволяющих всесторонне анализировать проблемы принятия решений в условиях неопределённости.

Можно выделить три основных подхода к построению моделей процесса принятия решений

§ теорию статистических решений;

§ теорию полезности;

§ теорию игр.

Эти теории нашли применение в психологической практике.

Теория принятия решений моделирует поведение людей, которые, принимая решения, действуют в соответствии с некоторыми аксиомами. В основе теории принятия решений лежит предположение о том, что выбор альтернатив должен определяться двумя факторами:

1) представлениями лица, принимающего решение о вероятностях различных возможных исходов, которые могут иметь место при выборе того или иного варианта решения;

2) предпочтениями, отдаваемыми различным исходам.

Первое – субъективная вероятность, второе – ожидаемая полезность.

Основы современной теории полезности были заложены А.Крамером и Д.Бернулли (1738), которые предположили, что для многих людей полезность богатства увеличивается с убывающей скоростью по мере его роста. Лишь в 1931г. философ и математик Ф.Рамсей построил систему аксиом для субъективно ожидаемой полезности. Опираясь на его результаты, Л.Сэвидж (1964) ввел строгую систему аксиом для субъективно ожидаемой полезности, которая формируется из аксиом предпочтения. Теория предпочтения основывается на отношении нестрогого 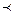«y не предпочтительнее, чем x» или строгого предпочтения 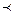«x предпочтительнее, чем y» (G.Fishburn, 1972). В последних работах чаще используется строгое предпочтение. Функция U называется функцией полезности для отношения предпочтения 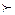на X, если u(x) > u(y) для любых x и y, таких, что x 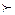y.

В настоящее время модель Севиджа для субъективно ожидаемой полезности получила наибольшее признание среди теорий принятия решений с риском: SEU = P* U, где SEU – субъективно ожидаемая полезность исхода; U –полезность наступившего исхода; P* - субъективная вероятность наступившего исхода. Субъективная вероятность – число, выражающее степень возможности данного события (по мнению субъекта).

С.Стивенс и Е.Галантер (1957) получили линейную функцию субъективной вероятности с искажениями на концах шкалы. Позже А.Тверски и Д.Канеман (1974) показали, что люди недооценивают низкие вероятности и переоценивают высокие.

В теории максимизации принимаются аксиомы, комбинирующие субъективную вероятность и полезность.

В теории принятия решений оценки вероятностей, полученные на основе суждения одного лица, входят в сумму 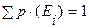, где E_i (i = 1, 2, …, n) полный набор взаимоисключающих событий, и если она не равна единице, то меняются рассматриваемые оценки [Keeney, 1974]. Для оценки распределения вероятностей величин, имеющих большое количество значений, берётся несколько значений точек функции распределения этой величины, и находится кривая, оптимально проходящая через эти точки.

Существуют четыре важных этапа процесса принятия решений:

1) определение альтернативных способов действия;

2) описание вероятностей возможных исходов;

3) ранжирование предпочтений возможных исходов через их полезность;

4) рациональный синтез информации, полученной на первых трёх этапах.

Дата добавления: 2014-01-20