Алгоритм Флойда - поиск всех кратчайших путей в графе

Алгоритма Дейкстры позволяет при доведении до конца построить ориентированное дерево кратчайших путей от некоторой вершины.

Метод Флойда позволяет найти длины всех кратчайших путей в графе.

Таким образом, метод Флойда может быть решен многократным применением алгоритма Дейкстры (каждый раз последовательно выбираем вершину от первой до N-ной, пока не получим кратчайшие пути от всех вершин графа), однако реализация подобной процедуры потребовала бы значительных вычислительных затрат.

Суть алгоритма Флойда заключается в проверке того, не окажется ли путь из вершины i в вершину j короче, если он будет проходить через некоторую промежуточную вершину.

Пусть вершины графа пронумерованы от 1 до n и введено обозначение 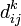для длины кратчайшего пути от i до j.

Очевидно, что 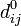— длина (вес) ребра (i, j), если таковое существует (в противном случае его длина может быть обозначена как ¥).

Существует два варианта значения :

1. Кратчайший путь между i, j не проходит через вершину k, тогда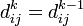

2. Существует более короткий путь между i, j, проходящий через k, тогда он сначала идёт от i до k, а потом от k до j. В этом случае, очевидно,

Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.

Тогда рекуррентная формула имеет вид: 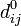— длина ребра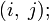

Алгоритм Флойда-Уоршелла последовательно вычисляет все значения для k от 1 до n. Полученные значения являются длинами кратчайших путей между вершинами i, j.

Очевидно, что сложность алгоритма есть O(n³). В монографии [Липский,1988] отмечено, что "для общего случая (т.е. без предположения о неотрицательности весов или о бесконтурности графа) не известен ни один алгоритм нахождения расстояния между одной фиксированной парой вершин, который был бы значительно эффективнее алгоритма нахождения расстояний между всеми парами вершин."

Дата добавления: 2014-01-20