Введение в теорию графов

Предлагается разделить (условно) терминологию теории графов на:

- геометрическую,

- теоретико-множественную,

- матричную.

Одно и то же понятие теории графов тогда будет можно формулировать на трех "языках". Так, например, определение графа:

Геометрическое - графом называется фигура, состоящая из точек (называемых вершинами) и отрезков, соединяющих некоторые из этих вершин. Соединяющие отрезки могут быть направленными (дугами), ненаправленными (ребрами), прямолинейными или криволинейными. Отрезок, соединяющий вершину с самой собой, называется петлей.

Теоретико-множественное - графом называется пара (V,R), где V – это множество вершин или узлов, R – это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами. Обозначается граф обычно через G(V,R).

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | R | — размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) ребра r = {u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Ребро называется петлёй, если его концы совпадают, то есть r = {v,v}.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v ® w ведёт от вершины v к вершине w.

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i (i=1,…,k), для которой все пары (v_i,v_{i + 1}) (i=1,…,k-1) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются.

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Матричное - графом называется множество (класс) квадратных (0,1)-матриц, перестановочно подобных между собой.

Первое и самое простое задание графа - это представление его с помощью картинки в соответствии с геометрическим определением графа. При этом в соответствии с договоренностью выше, вершинам конкретного представления графа будут приписаны номера.

Так на рисунке 1 даны два представления одного и того же графа.

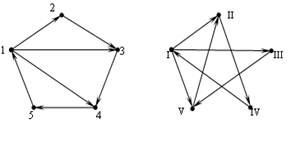
Рисунок 1.

Другое задание графа - списком. Можно считать, что в соответствии с теоретико-множественным определением графа все элементы множества RÍV´V, входящего в определение, упорядочены сначала по первым элементам пар, а затем по вторым, в соответствии с нумерацией вершин. Тогда два представления графа с рисунка 1 будут заданы двумя списками:

1 2, 3, 4 I II, III, V

2 3 II IV

3 4 III V

4 5 IV I

5 1 V II

В первом столбце - первые элементы пар, затем по строкам, списком через запятую, идут вторые элементы.

Третье задание графа - матрицами. Ниже выписаны две матрицы - A и B, задающие два представления графа с рисунка 1:

Дата добавления: 2014-01-20