Лекция 3. Непрерывные случайные величины (НСВ)

Непрерывные случайные величины (НСВ).

Определение 7. Случайная величина называется непрерывной, если ее функция распределения непрерывна на всей числовой оси и дифференцируема кроме, быть может, конечного числа точек.

Из этого определения и формулы (6) следует 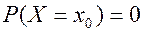, т.е. для НСВ вероятность того, что она примет одно, заданное определенное значение равна нулю. Поэтому для НСВ справедливы равенства:

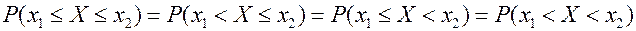(8)

Очевидно, что с учетом вышеизложенного, описание НСВ с помощью ряда распределения теряет смысл.

Определение 8. Плотностью распределения вероятностей 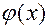(или дифференциальной функцией распределения) непрерывной случайной величины называют первую производную от ее функции распределения:

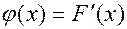(9)

Формула (9) определяет, так называемую, дифференциальную связь между функциям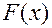ии .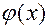

Замечание. Так как функция распределения дискретной случайной величины имеет ступенчатую форму, для ее описания плотность распределения неприменима.

График функции 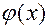называется кривой распределения.

Свойства плотности распределения вероятностей.

1) ,

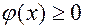2) ,

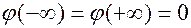3) 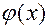- кусочно непрерывная функция

4) 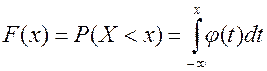(10)

Формула (10) определяет, так называемую, интегральную связь между функциям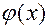и и 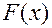. Функцию 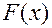иногда называют интегральной функцией распределенияили интегральным законом распределения.

5) 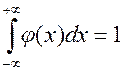(11)

Заметим, что (12) для НСВ является аналогом формулы (1) для ДСВ.

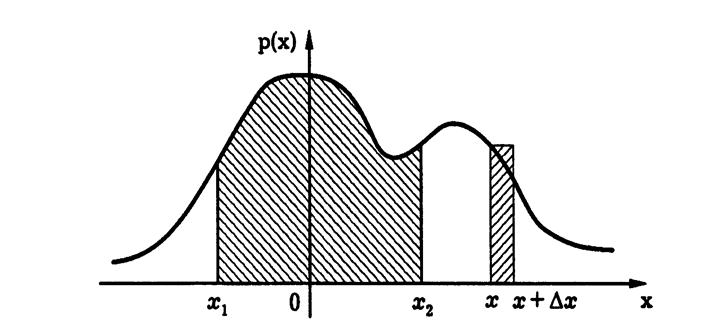
Геометрически свойства 1) и 5) означают, что график плотности распределения лежит не ниже оси Ox и площадь под графиком плотности равна 1.

6) Вероятности попадания НСВ X в интервал, отрезок или полуинтервал с одними и теми же концами одинаковы и равны определенному интегралу от плотности вероятности на этом промежутке:

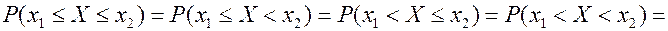
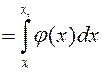(12)

Из (12) следует, что геометрически вероятность 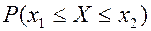представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности и отрезками прямых , , .

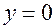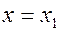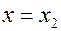Если 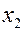близко к 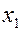, промежуток мал и площадь криволинейной трапеции можно заменить площадью прямоугольника. Мы получим, что вероятность попадания непрерывной случайной величины в интервал 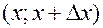приближенно равна .

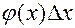Вероятностный смысл плотности распределения заключается в следующем. Плотность 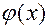непрерывной случайной величины 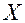равна вероятности попадания в малый интервал 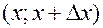, отнесенный к длине этого интервала.

Дата добавления: 2014-01-20