Материалы к лекции

Эксцентриситет кривой второго порядка (конического сечения) – число, равное отношению расстояния от любой точки кривой 2-го порядка до фокуса к расстоянию от этой точки до соответствующей директрисы.

Напоминание

РИС. 3-14

У эллипса две директрисы (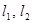), каждая соответствует своему фокусу 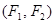; эксцентриситет: 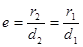. Уравнение директрис: 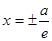; 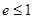. Если 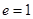, то 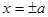и эллипс вырождается в прямую 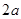. Если 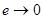, то директриса удаляется в бесконечность, фокусы сливаются в один. Эллипс превращается в окружность.

Итак, малость эксцентриситетов орбит планет Солнечной системы позволяет считать их орбиты круговыми.

Пусть одна планета имеет массу 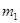, круговую орбиту радиуса 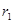и период обращения , вторая планета - .

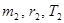Стационарное состояние: центробежная сила равна и противоположно направлена силе притяжения:

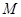, где - масса Солнца,

Гравитационная постоянная g =6,6710^-11 м³/кгс² или

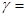(6.6732±0.0031)× 10^-8 дин×см­­­­²/г² [Н×м²/кг²].

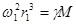- универсальная константа.

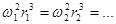Заменяя 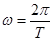, находим:

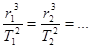или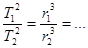

Для планет, движущихся по круговым орбитам, 3-ий закон Кеплера:

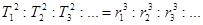
Мы знаем, что ускорение материальной точки (планеты) при равномерном движении по круговой орбите:

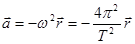. Подставим следующее обозначение: 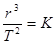(постоянная Кеплера); 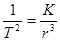; тогда 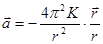и соответственно сила .

Поскольку планета и Солнце равноправно должны входить в закон взаимодействия:

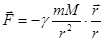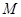, где - масса Солнца. Из сравнения сил видно, что

постоянная Кеплера .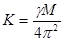

Ньютон не объяснил происхождения гравитационного взаимодействия – одной из фундаментальных сил природы. Общая теория относительности тоже не дает какого-либо наглядного толкования тяготения, дает лишь новый способ описания и более глубокое обобщение закона всемирного тяготения.

4 Лекция 4

ФИНАНСОВАЯ АКАДЕМИЯ

ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

В КОНЦЕ XX –НАЧАЛЕ XXI ВВ.(1992-2009 гг.)

Дата добавления: 2014-01-20