Решение. Найти допустимую область задачи линейного программирования, определяемую ограничениями (5)

Пример

Найти допустимую область задачи линейного программирования, определяемую ограничениями

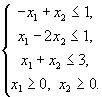
(5)

1. Рассмотрим прямую -х₁+х₂ = 1. При х₁=0 х₂ = 1, а при х₂ = 0 х₁=-1. Таким образом, эта прямая проходит через точки (0,1) и (-1,0). Беря х₁= х₂ =0 получим, что -0+0<1 и поэтому интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4а.

2. Рассмотрим прямую х₁-2х₂ = 1. При х₁=0 х₂ = -1/2, а при х₂ = 0 х₁=1. Таким образом, эта прямая проходит через точки (0, -1/2) и (1,0). так как 0-2·0 < 1 (4.б).

3. Наконец, рассмотрим прямую х₁+ х₂ =3. Она проходит через точки (0,3) и (3,0) и так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.в).

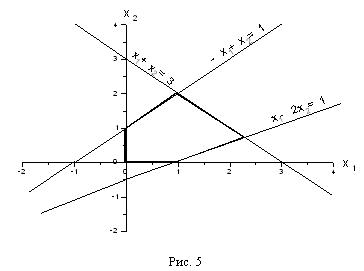
Сводя все вместе и добавляя условия х₁ ≥0, х₂ ≥0 получим рисунок 5, где выделена область, в которой выполняются одновременно все ограничения (5). Обратите внимание на то, что получившаяся область имеет вид выпуклого многоугольника.

Вернемся теперь к общему случаю, когда одновременно выполняются неравенства:

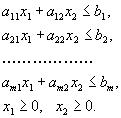
(6)

Имеют место некоторые случаи, которые тут могут получится.

1. Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 6).

2. Неосновной случай -получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 7. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение х₁+ х₂≤ 3. Оставшаяся часть будет неограниченным выпуклым многоугольником.

3. Наконец, возможен случай, когда неравенства (6) противоречат друг другу, и допустимая область вообще пуста.

Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще целевая функция
с₁ х₁+с₂ х₂→ max.

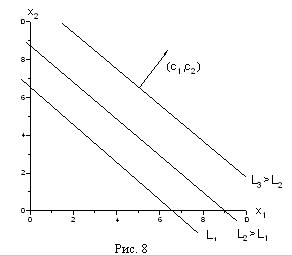
Рассмотрим прямую с₁ х₁+с₂ х₂=L. При увеличении L прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором (с₁ ,с₂), так как это - вектор нормали к нашей прямой и одновременно вектор градиента функции f (х₁, х₂)=с₁ х₁+с₂ х₂.

А теперь сведем всё вместе. Итак, надо решить задачу:

х₁ ≥0, х₂ ≥0

Ограничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая с₁ х₁+с₂ х₂=L пересекает допустимую область. Это пересечение дает какие-то значения переменных (x₁ ,x₂), которые являются планами.

Увеличивая L, мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (рис. 9). В конце концов эта прямая выйдет награницу допустимой области - как правило, это будет одна из вершин многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение прямой с₁ х₁+с₂ х₂=L с допустимой областью будет пустым.

Поэтому то положение прямой с₁ х₁+с₂ х₂=L, при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.

Дата добавления: 2014-01-20