Свойства внутренних сил системы

Главный вектор внутренних сил системы равен нулю

Главный момент внутренних сил системы относительно некоторого неподвижного центра равен нулю.

=

Движение системы характеризуется не только силами, действующими на нее, но и характером распределения масс в этой системе.

Центр масс системы – геометрическая точка, положение которой определяется радиус-вектором .

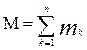, где (1)

Координаты центра масс по осям равны:

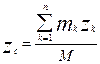; ; (2)

Пусть в систему входят n точек, для каждой точки запишем второй закон Ньютона:

; ;…;

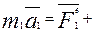
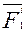
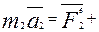
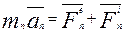
(3)

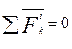
Выясним выражение в левой части равенства:

Возьмем от выражения (1) первую и вторую производные:

; ; ;

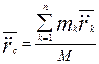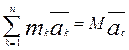
Полученный результат подставляем в (3):

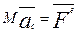(4)

- т еорема о движении центра масс системы: центр масс системы движется также, как точка, масса которой равна массе всей системы под действием сил, приложенных к системе.

Для решения задач запишем теорему в проекциях на оси координат:

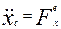M ; M ; M .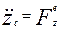

Рассмотрим частный случаи теоремы:

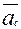Если в выражении (4) =0, тогда и =0;

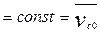
(начальная скорость центра масс)

Вывод: в этом случае центр масс движется равномерно и прямолинейно.

Если 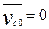, тогда 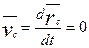, где .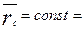

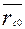Частные случаи через проекции на оси координат:

Если , тогда ; .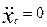

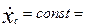
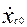Если 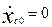, тогда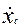 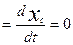; - закон сохранения координат центра масс относительно данной оси.

2. 1) Теорема для точки

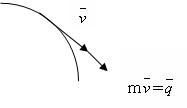
m 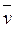-количество движения точки

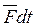– элементарный импульс силы

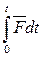=– полный импульс силы

Если , то ; ; ;

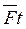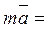
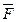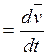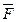(5)

Теорема об изменении количества движения точки и системы: производная по времени от количества движения точки равна приложенной силе.

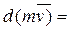
(6)

Дифференциал от количества движения точки равен элементарному импульсу силы.

=

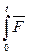
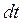
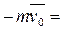
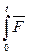
(полный импульс силы) (7)

– теорема в интегральной форме: изменение количества движения точки за некоторый промежуток времени равен импульсу силы за этот промежуток времени.

Частный случай теоремы: 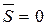, тогда - закон сохранения количества движения точки.

Следствие: , точка движется равномерно и прямолинейно.

Спроецируем (7) на оси координат:

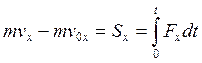
Частный случай через проекции на оси координат: если 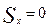, тогда ; ; 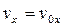точка движется равномерно относительно 0x, тогда если 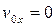, , 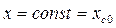то есть относительно оси 0x координата точки не изменяется.

2) Теорема для системы

Пусть система состоит из n точек, запишем второй закон Ньютона:

(8)

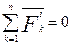
Выясним левую часть равенства (8), для этого возьмем производную по времени от выражения (1): , следовательно ;

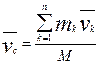(9)

; ; ;

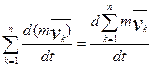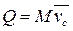
(10)

– количество движения системы.

(11)

– теорема об изменении количества системы в дифференциальной форме. Производная по времени от количества движения системы равна главному вектору внешних сил, приложенных к системе.

(12)

Дифференциал от количества движения системы равен элементарному импульсу внешних сил за определенный промежуток времени. Проинтегрируем (12):

(13)

– теорема в интегральной форме. Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, приложенных к системе за этот промежуток времени.

Вывод: так как внутренние силы в теорему не входят, то состояние системы нельзя изменить с помощью внутренних сил.

Частный случай теоремы: Пусть , тогда 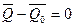; 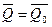, количество движения системы не изменится, закон сохранения количества движения системы.

Проекции на оси координат:

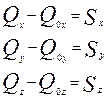(14)

Частный случай (14) на ось 0x: если 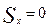, тогда 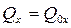, следовательно если , то ; .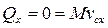

Дата добавления: 2014-01-20