Способность

Оценка 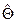называется способной оценкой параметра Ө, если она сходится по вероятности к оцениваемому параметру при неограниченном увеличении размера выборки n, т.е. при произвольном ε > 0

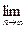Р{‌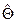│- Ө│≥ε } = 0

Несмещенность.

Оценка называется несмещенной оценкой параметра Ө, если среднее значение этой оценки по совокупности выборок х = (x₁, x₂,..., х_n) заданного размера в точности равняется оцениваемому параметру, т.е. если при любом n

m₁{ 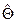} = g_Ө (х) W(х│Ө)dx = Ө_іст

Иначе говоря, для несмещенных оценок среднее значение ошибки 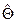- Ө равняется нулю.

Разность m₁{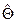}-Ө_іст=b_n(Ө) называют смещением оценки (систематической или средней ошибкой).

Примером несмещенной оценки среднего значения для произвольного распределения есть выборочное среднее. Выборочное среднее - способная и несмещенная оценка среднего значения начального распределения.

Достаточность.

Оценка называется достаточной оценкой параметра Ө распределения w₁(х│Ө), если условное распределение W (x₁, x₂,..., х_n │ Ө) не зависит от Ө. Из этого определения следует, что достаточная статистика содержит всю информацию о неизвестном параметре Ө, которую можно получить при наблюдениях.

Иначе говоря, для оценки параметра нет необходимости знать каждый из элементов выборки, а достаточно иметь лишь одну функцию выборочных значений - достаточную оценку (достаточную статистику).

Дата добавления: 2014-01-20