Интервальные оценки. Доверительный интервал и доверительная вероятность

Вследствие n наблюдений измеряемой величины А получаем оценку ее действительного значения А, равному среднему арифметическому х. Эта оценка также случайная величина. Нужно выяснить, в каких границах может изменяться действительное значение А при повторных измерениях величины в одних и тех же условиях, т.е. надо найти интервал значений, который с заданной вероятностью "накрывает" истинное значение измеряемой величины.

Такой интервал носит название доверительного, а заданная вероятность - доверительной. Доверительный интервал и доверительная вероятность характеризуют неопределенность результата измерения. Аналитически это записывается таким образом:

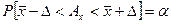
Это выражение читается так: истинное значение измеряемой величины А заключено в пределах доверительного интервала от к 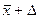с доверительной вероятностью α.

По аналогии случайная погрешность измерения заключена в пределах доверительного интервала от ∆₁ до ∆₂ с доверительной вероятностью α: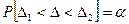

Доверительный интервал может быть как симметричным, так и несимметричным. Характер доверительного интервала зависит от формы плотности распределения случайной погрешности.

Для нормального распределения этот интервал симметричный. Половину симметричного доверительного интервала называют предельной погрешностью при доверительной вероятности α.

Предельную погрешность и доверительный интервал выражают через среднеквадратичное отклонение. Для нормального закона распределения доверительный интервал по заданной доверительной вероятности (и наоборот) определяют с помощью таблицы интеграла вероятности.

При симметричных распределениях доверительный интервал может быть определен в виде неравенств:

x - e < a < x + e

или

| a – x | < e

где x - среднее арифметическое значение.

Величина e определяется по заданной доверительной вероятности (надежности оценки) Р. Обычно надежность Р задается в виде одного из трех уровней: 0.95, 0.99, 0.999.

Далее будем рассматривать случай, если распределение описывается нормальной зависимостью. Рассмотрим два случая: если средняя квадратичная ошибка известна, если средняя квадратичная ошибка неизвестна.

Если заранее средняя квадратичная ошибка s известна, то доверительная оценка имеет вид

| a – x | < t(P)s /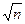

где n - число измерений, а значение t=t(P) определяется по заданной доверительной вероятности P из условия

2Ф(t) = P,

т.е. находится по таблице интеграла вероятности.

Таким образом, здесь

e = t(P)s /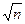

Если средняя квадратичная погрешность s заранее неизвестная, то вместо нее используют ее оценку

При этом доверительная оценка принимает вид

| a – x | < t(P; k) s /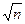

где множитель t(P;k) зависит уже не только от доверительной вероятности Р, но и от числа измерений n (k = n - 1).

Значение коэффициента t(P; k) табулированы и приведены в таблицах.

Таблицы составлены с помощью распределения Стьюдента, т.е. распределения вероятностей. Распределение Стьюдента зависит от одного параметра k = n - 1 и называется числом степеней свободы.

В практике обработки результатов измерений широкое распространение получило правило трех сигм:

Отклонение истинного значения измеренной величины от среднего арифметического значения результатов измерений не превосходит утроенной средней квадратичный погрешности измерений этого среднего значения.

Таким образом, правило трех сигм представляет собой доверительную оценку

| a – x | < 3s /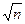

в случае известной величины s или доверительную оценку

| a – | < 3 s /

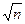
в случае неизвестной величины s.

Первая из этих оценокимеет надежность

независимо от количества измерений.

Надежность второй оценки существенным образом зависит от количества измерений n. Зависимость надежности P от количества измерений n для этой оценки приводится в таблицах.

Оценки точности измерений

Как и раньше будем предполагать, что ошибки измерения распределены по нормальному закону.

При известной дисперсии ошибки результата равноточных наблюдений (единичного измерения) s_набл ошибка результата измерения s_рез определяется выражением:

s_рез =

При неизвестной дисперсии ошибки результата равноточных наблюдений для оценки ошибки результата измерения используется предыдущее выражение, но в числителе стоит уже оценка среднеквадратичного отклонения s:

,

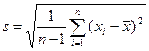и тогда

s_рез =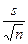

Дата добавления: 2014-01-20