Математическая формулировка задач об использовании сырья и привидение ее к канонической форме

Симплексные таблицы.

Алгоритм симплекс-метода для решения задач линейного программирования, заданных в канонической форме, обычно реализуется в виде так называемой симплекс-таблицы.

Пусть х₁ и х₂ – количества выпускаемых фирмой изделий А и В. Тогда условие производства (ограничение на запасы сырья) описываются системой неравенств вида:

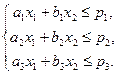
Объем выпущенной фирмой продукции в денежном выражении описывается целевой функцией:

.

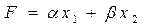В приведенных выше примерах задач линейного программирования допустимое множество описывалось различными способами: системами неравенств различных знаков, наборами равенств и, наконец, комбинациями равенств и неравенств. Такое разнообразие описаний является, с точки зрения теории, определенным недостатком, так как вынуждает каждый тип описания рассматривать по-своему. Однако все варианты постановок могут быть сведены к задаче линейного программирования, содержащей лишь равенства и условие неотрицательности переменных. Такая формулировка называется канонической.

Приведем эту задачу к канонической форме.

Переменными х₃, х₄, х₅ обозначим остатки сырья каждого вида (на момент окончания процесса производства). Тогда задачу можно представить в виде системы линейных уравнений:

(10)

Требуется найти такие неотрицательные значения переменной х₁,х₂, х₃, х₄, х₅, которые являются решение системы (10) и обеспечивают максимум целевой функции F.

Исходную симплекс-таблицу (S-таблицу) составляют из коэффициентов при переменных и свободных членов системы уравнений (10). При этом, переменные входящие в целевую функцию 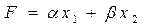будут являться свободными. В данном случае это х₁ и х₂. А остальные переменные (х₃, х₄, х₅) будут базисными. Результирующая S-таблица будет иметь следующую структуру:

Последнюю строку таблицы называют индексной строкой. Приведенная S-таблица является исходным базисным решением, совпадающим с началом системы координат.

Критерии наличия или отсутствия оптимального решения и критерии перехода к новой S-таблице.

При анализе S-таблицы на оптимальность пользуются следующими критериями:

1) если в индексной строке S-таблицы все элементы, находящиеся в столбцах свободных переменных отрицательны или равны нулю, то представленное в этой таблице решение является оптимальным.

2) если в S-таблице есть такой столбец свободной переменной, у которого элемент в индексной строке положителен, а все другие элементы этого столбца отрицательны или равны нулю, то решаемая задача оптимального решения не имеет.

Если оба этих критерия не выполняется (т.е. на пересечении индексной строки и столбца свободных переменных стоит положительный элемент и в этом же столбце есть хотя бы еще один положительный элемент), то выполняется условие перехода к новому более эффективному базисному решению, т.е. надо выполнить переход к новой S-таблице.

Алгоритм перехода к новой S-таблице включает следующие шаги:

1. Выбирают в исходной S-таблице «ключевой столбец», т.е. столбец свободной переменной, у которой элемент в индексной строке положителен (если таких столбцов несколько, обычно выбирают тот, которому соответствует больший элемент в индексной строке.

2. Определяют «ключевую строку», для этого делят элементы столбца p_i на соответствующие элементы ключевого столбца и выбирают строку, которой соответствует наименьшее частное.

3. На пересечении ключевых столбца и строки отмечают разрешающий элемент а*.

4. Определяют структуру новой S-таблицы, для этого свободную переменную соответствующую выбранному ключевому столбцу, вводят в базис вместо базисной переменной, соответствующей ключевой строке.

5. Каждый элемент ключевой строки исходной S-таблицы делят на а* и результат вносят в соответствующую строку новой S-таблицы.

6. Все оставшиеся клетки ключевого столбца заполняют нулями.

7. Те столбцы исходной S-таблицы, у которых в ключевой строке находятся нули, переносят в новую S-таблицу без изменений.

8. Все остальные элементы исходной S-таблицы преобразуют по правилу прямоугольника, и результаты преобразования вносят в соответствующие клетки новой S-таблицы.

«Правило прямоугольника»:

Для каждого элемента a_ij исходной S-таблицы, составим прямоугольник так, чтобы преобразуемый элемент a_ij и разрешающий элемент а* находились на противоположных вершинах прямоугольника (т.е. на одной из его диагоналей)

Новое значение элемента находим по формуле: a_ij*=a_ij–A*B:a*, где а * – разрешающий элемент, a_ij – исходное значение преобразованного элемента, А и В – элементы исходной таблицы, находящиеся в двух других вершинах прямоугольника.

9. В итоге получаем новую S-таблицу, которую опять проверяем на оптимальность. Если условие оптимальности не выполняется, то переходим к очередной S-таблице и так до тех пор, пока не будет получено оптимальное решение задачи, или доказано что такое решение не существует.

Замечание: На практике иногда встречаются случаи вырождения и зацикливания симплекс-метода.

Если свободный член p_i в ключевой строке S-таблицы будет равен нулю, то имеем вырожденный случай. Переход к новой S-таблице не приведет к улучшению плана. Если при преобразовании вырожденной S-таблицы снова получим вырожденную S-таблицу, то имеет место зацикливания алгоритма симплекс-метода.

Дата добавления: 2014-01-20