Обратная матрица. Матричные уравнения. Правило Крамера

3.1. Определение обратной матрицы. Мы по-прежнему будем рассматривать квадратные матрицы.

Определение. Пусть дана матрица А. Назовем матрицу 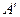правой обратной для А, если (– единичная матрица соответствующего порядка).

Аналогично, назовем левой обратной для А, если выполняется равенство .

Утверждение 1. .

Доказательство. Действительно,

Значит, можно говорить просто об обратной матрице. Будем ее обозначать А ^-1. Итак,

.

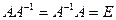Заметим, что не каждая матрица имеет обратную. Так как , то 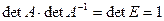, и если 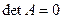(такие матрицы называются вырожденными), то матрица А не может иметь обратной матрицы.

Утверждение 2. Если обратная матрица существует, то она единственна. Иначе, если АВ = ВА = Е и АС = СА = Е, то В = С.

Доказательство:

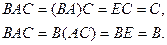
3.2. Существование обратной матрицы. Мы уже заметили, что если определитель матрицы равен нулю, то она не имеет обратной. Оказывается, что если определитель матрицы не равен нулю, то она имеет обратную матрицу. Мы сейчас ее построим.

Составим сначала матрицу из алгебраических дополнений:

.

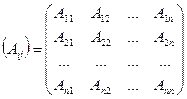Затем транспонируем эту матрицу:

.

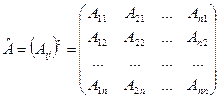Получившаяся матрица 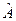называется присоединенной. Умножим 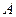на :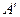

,

так как

.

(Вспомните замечание в конце предыдущей лекции.) Тогда .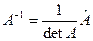

3.3. Матричные уравнения. Умея находить обратные матрицы, можно решать матричные уравнения. Например, чтобы решить уравнение АХ = В, где А и В - квадратные матрицы одинакового размера, причем А – невырожденная, достаточно умножить обе части равенства слева на А ^-1:

Аналогично, решением матричного уравнения ХА = В будет являться матрица Х = ВА ^-1.

3.4. Решение систем линейных уравнений с помощью обратной матрицы. Пусть дана система линейных уравнений с квадратной матрицей, т.е. количество уравнений равно количеству неизвестных. В матричном виде эту систему можно записать 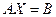. Если матрица А невырождена, т.е. ее определитель не равен нулю, то существует обратная матрица А ^-1, и тогда

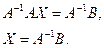
Мы получили решение такой системы линейных уравнений с помощью обратной матрицы и заодно показали единственность решения такой системы.

3.5. Правило Крамера в простейшем случае. Пусть дана система из двух линейных уравнений с двумя неизвестными:

Умножим первое уравнение на , а второе - на :

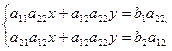
Вычитая из первого уравнения второе, получим выражение для неизвестной :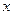

откуда, если ,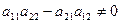

.

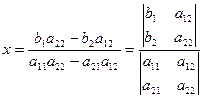Аналогично получается выражение для :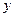

.

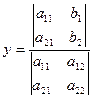Заметим, что в знаменателе обоих выражений стоит определитель матрицы коэффициентов, а в числителе – определитель, получившийся из матрицы коэффициентов заменой соответствующего столбца на столбец правых частей.

Оказывается, этот симпатичный результат можно обобщить на случай произвольного числа уравнений 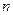. Напомним, речь идет только о системах линейных уравнений с квадратными матрицами коэффициентов.

3.6. Правило Крамера в общем случае. Пусть АХ = В - система линейных уравнений с квадратной матрицей коэффициентов, причем определитель матрицы 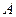не равен нулю. Тогда решением такой системы являются значения неизвестных

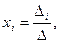
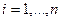
где 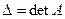, а 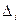- определитель матрицы, получившейся из матрицы 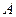заменой 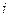-го столбца на столбец правых частей.

Покажем, что набор чисел 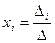действительно является решением системы.

Так как матрица А невырождена, то существует обратная матрица А ^-1. Умножим обе части равенства АХ = В слева на А ^-1, получим

.

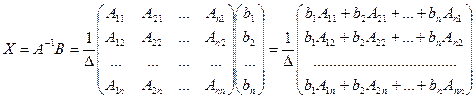Заметим, что 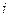-я компонента получившегося вектор-столбца - это разложение определителя 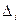по 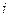-му столбцу. Значит,

.

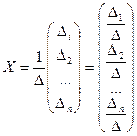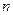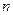Несмотря на привлекательность формулировки, практическое значение правила Крамера невелико: чтобы найти решение системы с неизвестными, приходится вычислять определитель -го порядка. Это оправдано при или .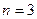

Дата добавления: 2014-01-20