Рельеф на топографических картах и планах

Рельефом называют совокупность неровностей местности естественного происхождения. На топографических картах рельеф обозначают с помощью горизонталей.

Горизонталь – это непрерывная кривая линия, соединяющая точки местности, лежащие на одной высоте. Каждую горизонталь можно представить как след сечения рельефа местности уровенной поверхностью.

Обычно такие сечения выполняют через определенный интервал по высоте h, который называется высотой сечения рельефа.

Высоты горизонталей H отсчитывают от исходной (нулевой) уровенной поверхности, и они везде кратны h.

Расстояние между горизонталями в плане называют заложением a, оно на плане уменьшается по мере увеличения крутизны склона.

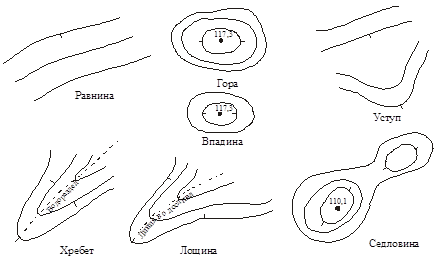Различают следующие формы рельефа: равнина, гора (холм), впадина (котловина), хребет, лощина, седловина, уступ (терраса) (Рисунок 21).

Рисунок 21 основные формы рельефа

Осевая линия, соединяющая самые высокие точки хребта, называется линией водораздела. А осевая линия лощины, по которой стекает вода, называется тальвегом (линией водослива). На горизонталях ставят бергштрихи по направлению падения склона.

Свойства горизонталей:

1. Они соединяют точки местности, лежащие на одной высоте.

2. Они не пересекаются и не раздваиваются.

3. Их высоты всегда кратны высоте сечения рельефа h.

4. При заданной высоте сечения h расстояния между горизонталями уменьшаются по мере увеличения крутизны склона.

5. Линии водораздела и водослива горизонтали пересекают под прямым углом.

Недостатки горизонталей:

1. Они не обладают наглядностью при изображении рельефа.

2. С их помощью нельзя изобразить любую форму рельефа (идеальную равнину, крутые и нависающие склоны, обрывы и др.).

3. При заданной высоте сечения рельефа его мелкие формы (меньше высоты h) не фиксируются на планах.

С учетом этих особенностей при изображении оврагов, промоин или обрывов используют специальные условные знаки (Рисунок 22), а для картирования слабо выраженного рельефа проводят дополнительные прерывистые горизонтали через половину или четверть высоты сечения (полугоризонтали или четвертьгоризонтали).

Для определения высоты Н горизонтали по отметке ближайшей к ней точки нужно знать высоту h сечения рельефа. Предположим, что на рис.1.17 h =5 м. На этом рисунке вершина горы расположена на высоте 117,3 м. Отметка ближайшей к ней горизонтали будет равна H =115 м, так как это число кратно высоте сечения и является ближайшим числом, меньшим отметки вершины 117,3 м.

В котловине ближайшая к точке дна горизонталь имеет отметку 120 м - это число кратно пяти метрам и больше отметки дна. На ровном склоне верхняя горизонталь имеет отметку 125 м, нижняя – 120 м. Если же одна из горизонталей снабжена отметкой (само число пишется так, чтобы верх цифры был обращен к вершине), то отметки соседних горизонталей можно определить, сообразуясь с высотой сечения рельефа и направлением бергштрихов.

На рисунке 24 при h =2 м H ₁=122 м, H ₂=124 м, H₃ =126 м.

Рисунок 24 определение высоты точки

Наконец, чтобы определить отметки точек, лежащих между горизонталями, поступают следующим образом. Сначала находят высоты горизонталей, между которыми расположена точка А на (Рисунок 24). Затем через эту точку проводят линию cb наибольшей крутизны как кратчайшее расстояние между горизонталями. Предполагая, что на протяжении этой лини отметка изменяется на высоту сечения рельефа h равномерно, оценивают на глаз превышение D h данной точки над горизонталью Н ₁ и прибавляют его к отметке этой горизонтали.

На рисунке 24 D h =0,8 м и Н _А=122+0,8=122,8 м. Для более точного определения отметки нужно измерить на карте отрезки Ас и bc, тогда

. (24)

Крутизну склонов, изображенных на карте, выражают либо углом наклона линии склона к горизонту n, либо уклоном i – тангенсом угла наклона этой линии:

, (25)

где Н _Аи Н _В - высоты конечных точек линии склона, d _АВ горизонтальное расстояние между точками.

Уклоны обычно выражают в сотых долях (процентах, %) от линии склона или тысячных долях (промиллях, ‰). Например, если tg n=0,025, то это составляет для уклона i =2,5% =25‰.

Для нахождения крутизны склона между соседними разноименными горизонталями измеряют заложение a, то есть расстояние по линии склона между этими горизонталями и, зная h, находят уклон

. (26)

Рисунок 25 График заложений

Для облегчения решения этой задачи под южной рамкой топографической карты построен график заложений, отражающий изменение заложения a от крутизны склона (при постоянном значении высоты сечения h). Так как согласно (26) , то для каждого заданного угла наклона n было вычислено соответствующее заложение a и построен график в масштабе карты (Рисунок 25). Для определения крутизны склона на заданном участке берут в раствор измерителя расстояние между соседними разноименными горизонталями и переносят его на график. На рисунке 25 n=2,8°.

Дата добавления: 2014-01-20