Модель идеального смешения (МИС)

Модель идеального вытеснения (МИВ)

Математическое моделирование структуры потоков

Наиболее корректной математической моделью структуры потоков в аппарате является исчерпывающее описание. Однако решение уравнений Навье – Стокса с условиями однозначности для большинства случаев невозможно. Поэтому на практике идут по пути упрощения модели, используя для характеристики структуры потока функцию распределения времени пребывания элементов потока в аппарате. Разумеется, f^*(Q) является далеко не полной характеристикой движения, хотя и достаточной для интегральной оценки работы аппарата.

Можно выделить две идеализированные модели, характеризующие предельные ситуации: идеальное вытеснение и идеальное смешение, а также более реалистичные модели промежуточного типа - ячеечная и диффузионная модели.

В аппарате частицы потока движутся параллельно друг другу с одинаковой скоростью w_X. Время пребывания в аппарате всех элементов потока одинаково. Введем понятие концентрации меченых элементов потока в аппарате. Средняя концентрация меченых элементов потока в аппарате определяется как:

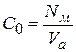, (2.147)

где N_M - количество помеченных элементов, V_a – объем аппарата.

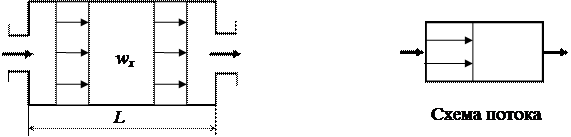Рис. 2.11 Модель идеального вытеснения

Исходное уравнение для МИВ получено из уравнения нестационарной конвективной диффузии (2.40):

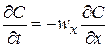. (2.148)

Результаты решения уравнения (2.148) представлены в безразмерной форме на рис. 2.12.

Рис. 2.12 Вид функции распределения f^*(Q) для МИВ

Поскольку все элементы движутся с одинаковой скоростью w_X, то у них одинаковое время пребывания в аппарате, совпадающее с 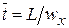. Поэтому .

Наиболее близка к МИВ структура турбулентного потока, движущегося по трубе при l/d>>1, цилиндрические аппараты небольшого диаметра, но значительной высоты, заполненные зернистым материалом.

Предполагается, что любая порция входящего в аппарат меченых элементов потока мгновенно и равномерно перемешивается во всем объеме. Таким образом, концентрация меченых элементов потока одинакова во всех точках аппарата. По аналогии с (2.31) (источника нет) можно записать:

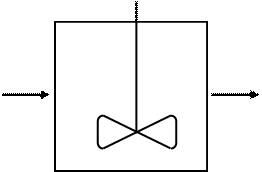Рис. 2.13 Модель идеального смешения (схема потока)

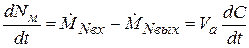, (2.149)

где 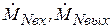– количество меченых элементов потока, входящих в аппарат и выходящих из него за единицу времени.

При любых значениях t>0, входа меченых элементов в аппарат не будет, т.е. . Тогда

. (2.150)

Имея, в виду 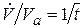получим:

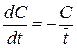и разделяя переменные:

. (2.151)

Интегрируя уравнение (2.151) с начальными условиями С(Q)=С₀ получим:

. (2.152)

Переходя, к безразмерной функции распределения имеем:

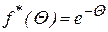. (2.153)

На рис. 2.14 изображена зависимость f^*(Q) от Q по формуле (2.153).

Рис. 2.14 Вид функции распределения f^*(Q) для МИС

К аппаратам идеального смешения близки аппараты с интенсивным перемешиванием и аппараты с псевдоожиженным слоем.

Структуры потоков в промышленных аппаратах не соответствует ни МИВ, ни МИС. Реальные аппараты промежуточного типа.

Дата добавления: 2014-01-20