Уровень Ферми

Для определения числа частиц, имеющих энергию в заданном интервале, помимо плотности квантовых состояний N(W) необходимо знать вероятность того, что данное состояние с энергией W занято частицей, т.е. нужно знать функцию распределения f (W). В условиях теплового равновесия для частиц с полуцелым спином, подчиняющихся принципу Паули, справедливо распределение Ферми – Дирака

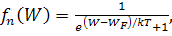
где k – постоянная Больцмана; Т – абсолютная температура; W_F – энергия Ферми или электрохимический потенциал, т.е. работа, которую необходимо затратить для изменения числа частиц в системе на единицу при условии постоянства объема и температуры.

Рассмотрим вид функции распределения Ферми – Дирака при различных температурах. Из формулы следует, что в случае Т = 0 в интервале энергии 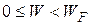имеем f _n = 1 и f _n = 0 для 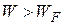. Это означает, что все квантовые состояния с энергией, меньшей энергии Ферми, заняты электронами, а уровни, лежащие выше уровня Ферми, полностью свободны, не заняты электронами. Следовательно, энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля.

Рассмотрим случай, когда Т > 0. Из распределения Ферми – Дирака для значения энергии, равной значению энергии Ферми (W = W_F), имеем f _n = 1/2. Таким образом, уровень Ферми есть энергетический уровень, вероятность наполнения которого при температуре, отличной от абсолютного нуля, равна 0,5. При Т > 0 часть электронов в результате теплового движения перейдет в состояния с энергией, большей энергии ферми (W > W_F), и соответственно часть состояний, находящихся ниже уровня Ферми, окажется свободной. В этом случае число частиц, перешедших на более высокие энергетические уровни, будет равно количеству образовавшихся свободных состояний в области W < W_F.

Произведем оценку области изменения функции распределения f _n (W) для случая Т > 0. Для этого подсчитаем f _n (W) для разных значений энергии. Для энергий, отличающихся от W_F на ± kT, значение на f _n (W) составляет (1+ е)^-1 = 0,27 и (1+1/ е)^-1 = 0,73. При W - W_F = ± 2 kT значения f _n равны 0,118 и 0,882, а при W - W_F = ± 3 kT – 0,047 и 0,953. Из этих данных следует, что вероятность заполнения состояний заметно отличается от единицы или нуля лишь в пределах (2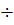3) kT вблизи значения W = W_F (рис. 1).

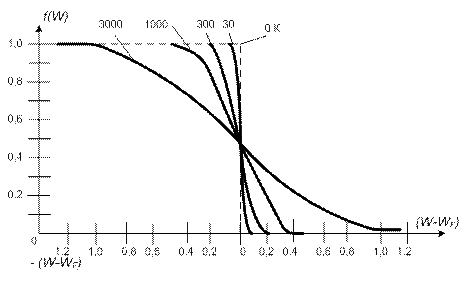
Рис. 1. Вид функции распределения Ферми – Дирака

Функция распределения Ферми – Дирака характеризует вероятность заполнения данного квантового состояния электроном. Вероятность того, что при тепловом равновесии в состоянии с энергией W электрон отсутствует, т.е. оно занято дыркой, будет равна:

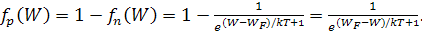
Следовательно, функция распределения для дырок аналогична функции распределения для электронов, если отсчитывать энергию дырок от уровня Ферми в противоположную сторону по сравнению с направлением отсчета энергии для электронов.

Для электронов, находящихся в состояниях с энергией W – W_F >> kT, выражения для f_n и f_p имеют вид:

,

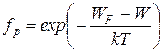
т.е. совпадают с функцией распределения Больцмана для частиц, подчиняющихся классической статистике. Если носители заряда подчиняются статистике Больцмана, то электронный газ невырожден и соответственно полупроводник с таким распределением носителей заряда принято называть невырожденным.

Таким образом, для большинства полупроводников (невырожденных)можно пользоваться статистикой Максвелла - Больцмана и только в некоторых случаях для полупроводников (вырожденных)необходимо использовать статистику Ферми - Дирака. Разница в этих двух функциях распределения электронов по энергиям показана на рис. 2.

Положение уровня Ферми в полупроводнике будет определять и дрейфовую и диффузионную составляющие тока.

Одно из фундаментальных положений физики твердого тела – постоянство (одинаковость) уровня Ферми для всех частей равновесной системы твердых тел, какой бы разнородной оно не была. Другими словами, в условиях равновесия, когда направленного движения носителей заряда нет, должно иметь место условие: 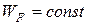, т.е. 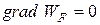, тогда ток в полупроводнике .

W-W_F (эВ)

f_n(W)

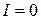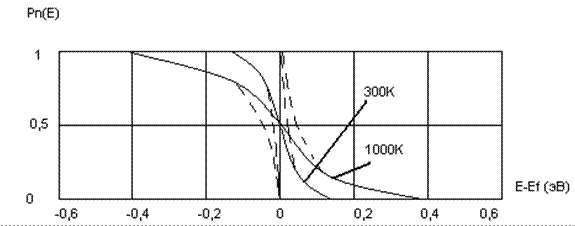
Рис. 2. Вероятность заполнения электронами энергетических уровней при различных температурах: сплошная – по статистике Ферми-Дирака, пунктир – по статистике Максвелла-Больцмана для электронов в зоне проводимости и в валентной зоне

Для собственного полупроводника уровень Ферми определяется выражением: ,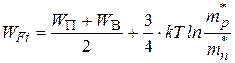

где 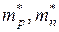– эффективная масса дырок и электронов соответственно.

При температуре абсолютного нуля уровень Ферми для собственного полупроводника лежит в середине запрещенной зоны. У собственного полупроводника скорость изменения уровня Ферми с температурой пропорциональна отношению эффективных масс дырок и электронов. В результате этого с повышением температуры уровень Ферми отдаляется от зоны с тяжелыми носителями заряда, приближаясь к зоне с легкими носителями заряда. Например, при 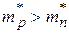уровень Ферми с повышением температуры линейно смещается к днй зоны проводимости. И если расстояние от уровня Ферми до этой зоны становится соизмеримо с kT, то в ней наступает вырождение и соответствующий интеграл Ферми – Дирака уже не может быть заменен экспонентой. При этом, чем сильнее различаются эффективные массы электронов и дырок, тем раньше наступает вырождение.

В случае 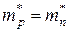положение уровня Ферми не зависит от температуры и определяется серединой запрещенной зоны: .

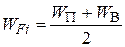Более точный анализ показывает, что сама ширина запрещенной зоны изменяется с температурой. Рост амплитуды тепловых колебаний атомов решетки приводит к ее уменьшению. Кроме того, с увеличением температуры изменяются межатомные расстояния, что также оказывает влияние на ширину запрещенной зоны. В результате зависимость Δ W з(Т) может иметь сложный характер. В качестве примера на рис. 3 показаны изменения ширины запрещенной зоны в зависимости от температуры для германия, кремния и арсенида галлия.

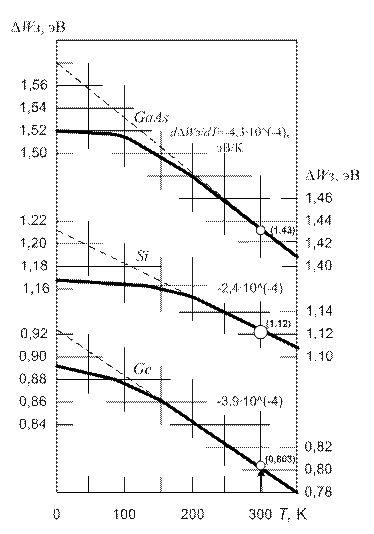
Рис. 3. Зависимость ширины запрещенной зоны германия, кремния и арсенида галлия от температуры

Для этих полупроводников значения ширины запрещенной зоны при 0 К составляют 0,89; 1,16 и 1,52 эВ соответственно. У них, как следует из рис. 3, в диапазоне температур 175 – 350 К ширина запрещенной зоны меняется линейно с температурой. При этом температурный коэффициент изменения ширины запрещенной зоны α = d Δ W з/ dT < 0 зависит от материала полупроводника (табл. 1). У PbS α < 0, ширина запрещенной зоны возрастает от 0,34 эВ при 0 К до 0,41 эВ при 300 К.

Таблица 1

Температурный коэффициент изменения ширины запрещенной зоны

	Германий	Кремний	Арсенид галлия	Антимонид индия
α, эВ/К	3,9∙10^-4	2,4∙10^-4	4,3∙10^-4	до 1750

В этих случаях зависимость подчиняется линейному закону вида

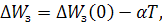
где Δ W з(0) – экстраполированная ширина запрещенной зоны при 0 К.

Теоретический анализ показывает:

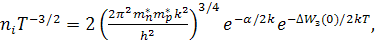
откуда следует, что

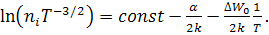
Таким образом, если ширина запрещенной зоны полупроводника линейно зависит от температуры, график зависимости ln(n_iT ^-3/2) от 1/ Т также представляет собой прямую линию, наклон которой характеризуется значением Δ W з(0), которое является экстраполированной шириной запрещенной зоны при 0 К. Истинное значение ширины запрещенной зоны полупроводника при данной температуре определяется по формуле .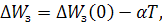

Для примесных полупроводников уровень Ферми можно определить из соотношений (справедливы для Т ≠ 0 К):

,

,

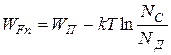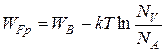где N_C, N_V – эффективная плотность разрешенных уровней в зоне проводимости и валентной зоне соответственно, N _Д, N _А – количество донорных и акцепторных уровней (степень легирования).

При решении задач удобнее использовать следующие соотношения (справедливы для Т ≠ 0 К):

,

.

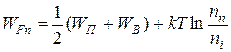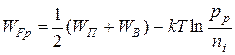Таким образом, положение уровня Ферми в примесных полупроводниках зависит от температуры, степени легирования и ширины запрещенной зоны.

Для определения поведения уровня Ферми в области низких температур необходимо уточнить функцию Ферми – Дирака для примесных полупроводников.

Рассмотрим полупроводник, содержащий донорную примесь с концентрацией N _Д. Если бы на примесном уровне согласно принципу Паули могли расположиться 2 электрона с антипараллельными спинами, то вероятность его заполнения определялась бы Ферми – Дирака

в которой вместо W следовало бы поставить W _Д – энергию электрона на уровне примеси. Но на уровне W _Д может быть только один электрон (атом донора может удержать один электрон), следовательно, нейтральное состояние донорной примеси имеет вдвое больший статистический вес по сравнению с ионизированным состоянием. Тогда вероятность нахождения электрона на донорном уровне с энергией W _Д будет определяться выражением

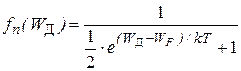
Предэкспоненциальный множитель 1/2 в общем случае можно записать через g ^-1. Таким образом, для одновалентной донорной примеси (может отдать для участия в проводимости только 1 электрон), примесный уровень двукратно вырожден и фактор (степень) спинового вырождения g = 2.

Аналогично для акцепторного полупроводника, например кремния, легированного бором. Нейтральный атом бора с соседними атомами кремния образует 3 ковалентных связи, четвертая связь одного из четырех соседних атомов кремния остается незавершенной, и она, располагаясь около атома бора, ведет себя как положительная дырка. В эту незавершенную связь может перейти электрон от соседнего атома кремния, и для этого потребуется энергия, равная W _А. В результате образуется свободная дырка, а атом бора превращается в отрицательно заряженный ион бора. Таким образом, на энергетическом уровне акцепторной примеси находится 1 электрон с произвольным направлением спина (нейтральное состояние акцепторной примеси) либо имеется 2 электрона с антипараллельными спинами, в случае когда атом акцепторной примеси для укомплектования парной связи захватывает электрон из валентной зоны (ионизированное состояние акцепторной примеси). Следовательно, степень вырождения акцепторного уровня g = 2.

В области низких температур (рис. 4) положение уровня Ферми будет определяться соотношением вида

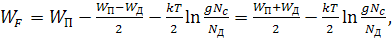
где – g фактор спинового вырождения,

а энергия активации будет:

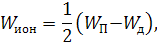
т.е. равна половине энергии ионизации донорной примеси. В невырожденном донорном полупроводнике при температуре абсолютного нуля уровень Ферми располагается посередине между дном зоны проводимости и уровнем донорной примеси.

Строгий теоретический анализ показывает, что в области достаточно низких температур (несколько градусов по шкале Кельвина), когда gN _c< N _Д, уровень Ферми вначале повышается до некоторого максимального значения, а затем начинает снижаться и при gN_c=N _d снова имеем W_F =1/2 (W_П + W_Д), как и для случая Т=0. Дальнейшее повышение температуры сопровождается ростом N_c и в области температуры, когда gN_c > N _Д, уровень Ферми продолжает снижаться. Такому перемещению уровня Ферми соответствует экспоненциальная температурная зависимость концентрации электронов

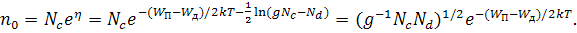
Эта область изменения уровня Ферми с температурой, которая описывается предыдущей формулой, является областью слабой ионизации примеси (или областью вымораживания). Она обозначена цифрой 1 на рис. 4, на котором проиллюстрировано изменение уровня Ферми и концентрации электронов в зависимости от температуры для донорного полупроводника.

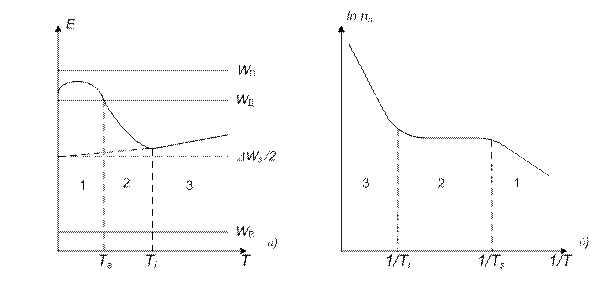
Рис. 4. Изменение положения уровня Ферми (а) и концентрации электронов (б) с температурой для донорного полупроводника

При дальнейшем повышении температуры концентрация электронов в зоне проводимости становится сравнимой с концентрацией примеси и предыдущие выражения для W_F и n_n в этом случае неприменимы. Однако теперь можно рассматривать другой крайний случай, когда температура достаточно высока и выполняется неравенство

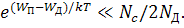
При этом функция Ферми аппроксимируется выражением 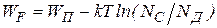, которому соответствует: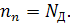

Это означает, что практически вся донорная примесь ионизирована, и концентрация электронов в зоне проводимости не зависит от температуры. Эта область температур, при которой имеет место полная ионизация примеси, носит название области истощения примеси (или область полной ионизации примеси) и на рис.4 отмечена цифрой 2.

Условие полной ионизации донорной примеси, когда n _n = N _Д, соответствует положению уровню Ферми на несколько kT ниже уровня примеси W _Д. Это значит, что при повышении температуры уровень Ферми, понижаясь, пересекает уровень W _Д и уходит вниз. Температура, при которой W_F = W _Д, носит название температуры истощения T_S, ее можно определить из условия

откуда

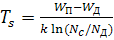
Как следует из выражения, температура истощения тем ниже, чем меньше энергия ионизации (W _П – W _Д), и концентрация донорной примеси N _Д и чем больше эффективная масса электронов, определяющая величину N_С. При малых значениях (W _П – W _Д) истощение примеси наступает при очень низких температурах. Например, в электронном германии, легированном сурьмой в количестве N_Д = 10¹⁶ см^-3, для которой энергия ионизации равна 0,0096 эВ, насыщение наступает уже при Т_S = 32К.

При дальнейшей повышении температуры увеличение концентрации электронов в зоне проводимости будет осуществляться за счет переходов электронов из валентной зоны. В этом случае положение уровня Ферми и концентрация электронов будут определяться уравнениями для W_Fi. и n_i. На рис. 4 область 3 соответствует области собственной проводимости. В этом случае W_Fi и можно определить

Отсюда получаем

Анализ этого выражения показывает, что температура T_i, при которой наступает собственная проводимость у донорного полупроводника, тем ниже, чем меньше ширина запрещенной зоны и концентрация примеси и чем больше значение эффективных масс носителей заряда.

Таким образом, используя описанные приближения, можно проследить изменение концентрации электронов и положения уровня Ферми в запрещенной зоне электронного полупроводника во всей области изменения температуры.

В качестве примера на рис. 5 приведены температурные зависимости уровня Ферми и концентрация равновесных электронов n ₀ и дырок р ₀ для германия, легированного сурьмой в количестве N_Д ≈ 10¹⁶ см^-3. Кроме того, на этих кривых пунктиром показан ход W_Fi и n_i в собственном германии. При построении графиков учтена зависимость ширины запрещенной зоны германия от температуры.

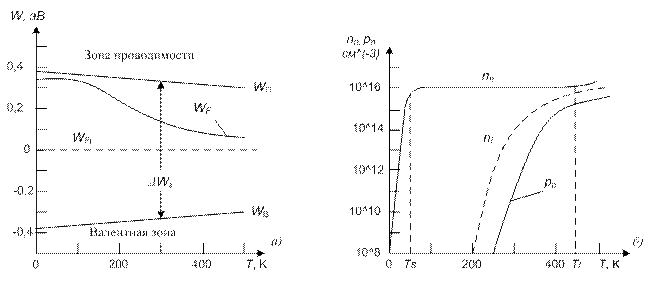
Рис. 5. Температурная зависимость уровня Ферми (а) и концентрации носителей заряда (б) для германия, легированного сурьмой

Из этого рисунка следует, что при температуре абсолютного нуля уровень Ферми в германии расположен посередине между дном зоны проводимости W_П и уровнем донорной примеси W_Д. При повышении температуры он опускается и приближается к уровню примеси W_Д. При температуре насыщения T_S на донорной примеси электроны находятся в количестве, равном:

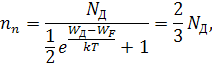
а в зоне проводимости соответственно 1/3 N _Д электронов. С дальнейшим ростом температуры уровень Ферми продолжает опускаться и наступает область истощения; вся примесь ионизирована, и концентрация электронов проводимости остается постоянной и равной n_n = N _Д. В этой температурной области имеет место уже ионизация атомов основного вещества, и появляются неосновные носители заряда – дырки. Их концентрация резко возрастает с ростом температуры согласно соотношению

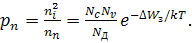
Когда уровень Ферми достигает середины запрещенной зоны, то n_n = p_n = n_i и полупроводник от примесного переходит к собственному. При дальнейшем повышении температуры уровень Ферми приближается к той зоне, которая имеет меньшую эффективную плотность состояний.

Уровень Ферми для кремния в зависимости от концентрации примесей и температуры приведен на рис. 6. Здесь же приведена зависимость ширины запрещенной зоны от температуры.

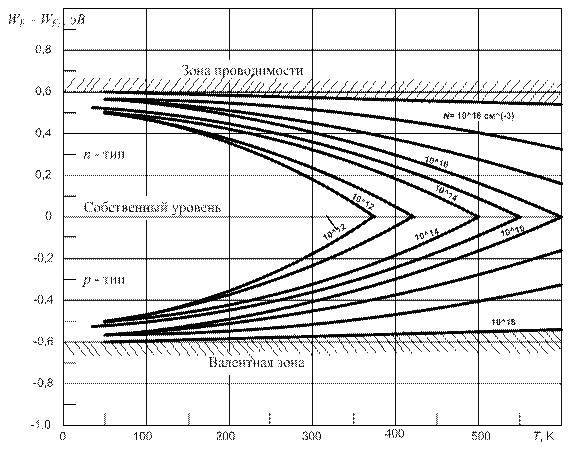
Рис. 6. Зависимость уровня Ферми в кремнии от температуры и концентрации примесей

В акцепторном полупроводнике, как и в случае донорной примеси, при высоких температурах наступает область истощения, характеризующаяся полной ионизацией атомов акцепторной примеси. С дальнейшим ростом температуры уровень Ферми поднимается к середине запрещенной зоны, и полупроводник ведет себя как собственный.

Выводы:

1. При Т = 300ºК уровень Ферми в n-полупроводнике лежит, как правило, ниже уровня донорной примеси W _Д, но выше середины запрещенной зоны.
В p-полупроводнике уровень Ферми расположен выше уровня акцепторной примеси W _А, но ниже середины запрещенной зоны.

2. Чем сильнее легирован полупроводник n-типа, тем ближе уровень Ферми к дну зоны проводимости, для p-типа: чем больше акцепторной примеси, тем ближе уровень Ферми к валентной зоне. Таким образом, чем сильнее легирован полупроводник, тем ближе уровень Ферми к зоне, отвечающей за тип проводимости (зона основных носителей заряда).

3. С ростом температуры уровень Ферми в n-полупроводнике снижается к середине запрещенной зоны, а в p-полупроводнике повышается к середине запрещенной зоны, т.е. примесный полупроводник ведет себя как собственный.

4. Чем сильнее легирован материал, тем выше максимальная рабочая температура прибора, использующего примесный характер полупроводника.

Дата добавления: 2014-01-20