
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ой тип задачи
|
|
|
|
Стационарное распределение температуры в бесконечном однородном цилиндре, у которого образующие  , направляющая лежит в плоскости
, направляющая лежит в плоскости  , а боковая поверхность поддерживается при определенной температуре
, а боковая поверхность поддерживается при определенной температуре  ,
, 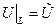 и тоже остается постоянной на любой прямой,
и тоже остается постоянной на любой прямой,  , проходящей в цилиндре, так что
, проходящей в цилиндре, так что  .
.
Наиболее простая задача Дирихле в одномерном случае. Тогда уравнение Лапласа в декартовых координатах
 , его решение
, его решение 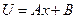
(стационарное распределение температуры в тонком стержне с теплоизолированной боковой поверхностью всегда линейно)
Задача Дирихле имеет решение в этом случае 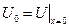 ,
, 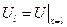 .
.
В следующей задаче с осевой симметрией – уравнение Лапласа в цилиндрических координатах, считая, что  не зависит от
не зависит от 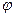 и
и 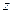 :
:
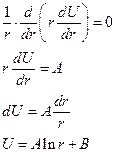
Задача Дирихле  имеет решение
имеет решение

Эта формула дает решение задачи о стационарном распределении тепла в пространстве между двумя цилиндрами с осью при условии, что на поверхности цилиндров поддерживается постоянная температура. Полученное решение теряет смысл при 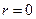 .
.
Если  зависит только от расстояния точки до начала координат, то воспользуемся сферическими координатами:
зависит только от расстояния точки до начала координат, то воспользуемся сферическими координатами:
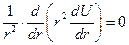
отсюда
 задача Дирихле:
задача Дирихле: 
Стационарное распределение температуры в сферическом слое 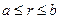 :
:

при 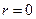 - решение не имеет смысла.
- решение не имеет смысла.
Трехмерная и двухмерная задачи Дирихле может быть точно решена только для сравнительно простых областей.
МЕТОД ФУНКЦИИ ГРИНА ДЛЯ ЗАДАЧИ ДИРИХЛЕ
Этот метод базируется на формуле Грина, является следствием формулы Остроградского-Гаусса:
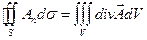 ;
;
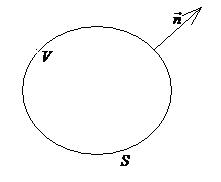
где  - граница области
- граница области 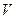 ,
,  - единичный вектор нормали
- единичный вектор нормали  ;
;
Пусть  и
и 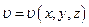 - две любые дважды дифференцируемые функции и
- две любые дважды дифференцируемые функции и
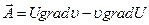 ,
,
Тогда
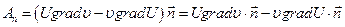 ;
;
Т.к. 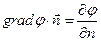 , то
, то 
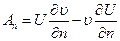 .
.
Вычислим 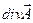 :
:
 ;
;
преобразуем каждое выражение в правой части:
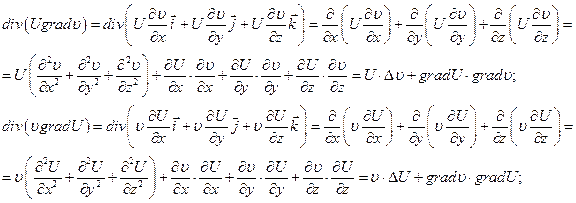
Следовательно, 
Подставим  и
и  в формулу Грина.
в формулу Грина.

 - формула Грина.
- формула Грина.
Пусть область  ограничена снаружи замкнутой поверхностью
ограничена снаружи замкнутой поверхностью  и изнутри замкнутой поверхностью
и изнутри замкнутой поверхностью  , лежащей целиком внутри
, лежащей целиком внутри  . Формулу Остроградского-Гаусса запишем в виде:
. Формулу Остроградского-Гаусса запишем в виде:
 , где
, где  - единичный вектор внешней нормали к
- единичный вектор внешней нормали к  , то есть,
, то есть,  направлен внутрь
направлен внутрь  .
.
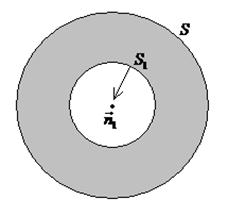
Соответственно формула Грина примет вид:
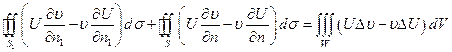
Эта формула – основа метода функции Грина для решения задачи Дирихле в пространстве.
Введем понятие самой функции Грина для трехмерного случая:

В качестве поверхности  возьмем границу области
возьмем границу области  , для которой решаем задачу Дирихле, и выберем внутри произвольную, но фиксированную точку
, для которой решаем задачу Дирихле, и выберем внутри произвольную, но фиксированную точку  , которую окружим сферой
, которую окружим сферой  радиуса
радиуса  >0 с центром в точке
>0 с центром в точке  . При этом, предположим, что сфера
. При этом, предположим, что сфера  и
и  имеет область
имеет область  . Обозначим через
. Обозначим через  - любую точку области
- любую точку области  , отличную от
, отличную от  ,
,  - расстояние между точками
- расстояние между точками  и
и  :
:
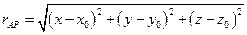
Функция  - гармоническая, то есть удовлетворяет уравнению Лапласа
- гармоническая, то есть удовлетворяет уравнению Лапласа 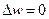 во всех точках, кроме точки
во всех точках, кроме точки  , в ней она обращается в бесконечность.
, в ней она обращается в бесконечность.
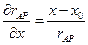 ;
; 
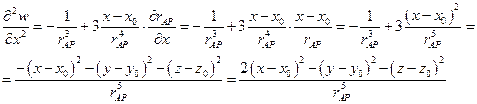
Аналогично получим:

Суммируем:

 функция
функция  является гармонической.
является гармонической.
Обозначим далее через 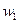 - решение задачи Дирихле для области
- решение задачи Дирихле для области 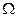 с краевыми условиями
с краевыми условиями
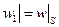
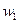 - гармоническая функция во всей области
- гармоническая функция во всей области 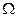 , включая сферу
, включая сферу  и точку
и точку 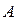 . Рассмотрим это на примере.
. Рассмотрим это на примере.
Пусть 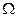 - шар радиуса 1 с центром в начале координат,
- шар радиуса 1 с центром в начале координат,  - его граница и точка
- его граница и точка 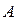 совпадают с началом координат.
совпадают с началом координат.
Тогда
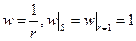
В то же время функция, принимающая на границе значение, равное 1 и гармоническая во всем шаре, будет тождественно равно 1
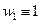
Физическое соображение: если температура в точках тела не меняется с течением времени, а на границе тела постоянна, то она будет величиной постоянной.
Вывод из примера: функции 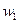 и
и 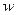 совпадают только на границе.
совпадают только на границе.
Разность функций 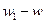 называется функцией Грина для области
называется функцией Грина для области 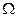 :
:
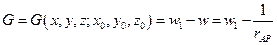
Функция Грина на границе обращается в нуль:

Пусть  - искомая гармоническая функция в области
- искомая гармоническая функция в области 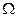 , принимает на границе значение
, принимает на границе значение  :
:  ,
,
положим 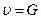 и применим к области
и применим к области  формулу Грина:
формулу Грина:
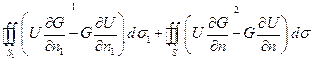 >0,
>0,
т.к. 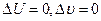 ;
; 
2: 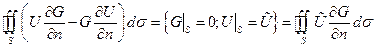 ;
;
1: введем сферические координаты  с началом в точке
с началом в точке 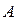 проинтегрируем по
проинтегрируем по  :
:
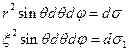 ;
; 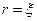


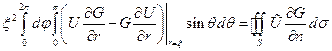
 ;
; 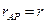 ;
;  ;
;
правая часть равенства не зависит от  , поэтому она должна быть равна пределу левой части при
, поэтому она должна быть равна пределу левой части при 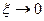 :
:

Функции  и
и 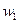 - гармонические во всей области
- гармонические во всей области 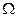 , включая точку
, включая точку 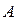 , поэтому они вместе со своими производными ограничены, это значит, что
, поэтому они вместе со своими производными ограничены, это значит, что

 и
и 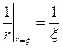 - неограниченна при
- неограниченна при 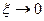 .
.
Найдем предел каждого слагаемого в отдельности:

Т.к. функция  непрерывна, то
непрерывна, то  считая возможным переход к пределу под знаком интеграла, получим
считая возможным переход к пределу под знаком интеграла, получим
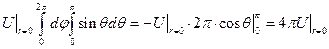
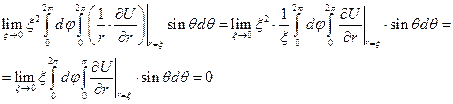
Таким образом,

Т.к. при 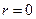 в качестве аргументов функции
в качестве аргументов функции  мы получим координаты точки
мы получим координаты точки 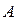 , то
, то 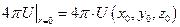 , то
, то
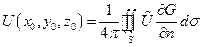 - решение задачи Дирихле в пространстве, если известна
- решение задачи Дирихле в пространстве, если известна  - функция Грина получаем значение искомой функции и в любой точке
- функция Грина получаем значение искомой функции и в любой точке 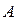 области
области 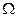 .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 403; Нарушение авторских прав?; Мы поможем в написании вашей работы!