Момент количества движения и момент силы относительно неподвижной оси

Рассмотрим неподвижную ось 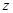. Пусть относительно некоторой точки О, лежащей на этой оси, момент количества движения - 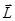, а момент силы - .

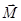РИС. 3-15

Моментом количества движения (или моментом импульса) относительно оси 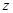называют проекцию на эту ось вектора 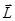, определенного относительно произвольной точки на оси: .

Аналогично вводится понятие момента силы относительно данной оси: .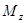

Свойства этих величин выясним, спроектировав на ось 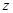уравнение моментов:

.

Производная по времени момента количества движения относительно некоторой оси 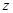равна моменту силы относительно этой же оси.

В частности, если , то .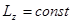

Если момент силы относительно некоторой неподвижной оси 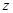равен нулю, то момент количества движения частицы относительно этой же оси остается постоянным.

При этом сам вектор 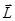может меняться! Например, может прецессировать вокруг оси. В качестве примера рассмотрим поворот вектора под действием силы тяжести.

РИС. 3-16

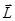- поворачивается под действием момента силы тяжести . Также момент силы перпендикулярен оси x, т.е. ее не пересекает:

.

Запишем аналитические выражения для и 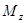, т. е. найдем проекции на ось 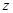векторных произведений и .

Введем цилиндрические координаты: .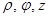

РИС. 3-17

Тогда:

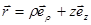- радиус-вектор от азимута не зависит (так как частица вращается вокруг оси Oz),

, подставим в выражение для момента количества движения с учетом правила векторного произведения:

(здесь учтен момент импульса, а также выражение для связи линейной и угловой скорости, здесь введена проекция угловой скорости по z, а также 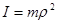- момент инерции материальной точки).

Аналогично введем:

, после подстановки в выражение для момента силы, с учетом векторного произведения, получаем:

(- проекция вектора силы 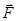на орт ).

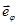Закон сохранения момента количества движения относительно оси можно записать также следующим образом:

если , то 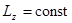и, следовательно, - сохраняется угловая скорость движения.

Для системы материальных точек, жестко связанных между собой, т. е. для твердого тела (жесткая связь – чтобы была для всех точек одна):

{это сумма моментов количества движения отдельных частиц}

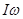=, где .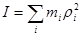

Дата добавления: 2014-01-20