Кинетическая энергия вращающегося тела. Кинетическая энергия частицы, находящейся на расстоянии от оси:

Кинетическая энергия частицы, находящейся на расстоянии 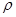от оси:

.

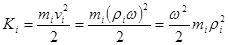Отсюда – кинетическая энергия всего вращающегося тела:

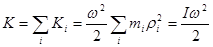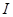, - момент инерции тела.

Таким образом, в механике вращательного движения момент инерции играет роль массы, а угловая скорость – роль линейной скорости в поступательном движении.

Работа сил, вращающих тело

Покажем, что работа сил, вращающих тело, за промежуток времени t равна .

Для этого надо вспомнить определение работы и вместо силы использовать выражение (с. 55), а вместо , т.е. использовать выражение для скорости и связь ее с угловыми характеристиками.

Для справки!

Вычисления моментов инерции: Стрелков С.П. «Механика», 1965 г. (§59).

Теорема Гюйгенса-Штейнера

Если известен момент инерции тела относительно оси, проходящей через центр масс, , то момент инерции относительно любой параллельной ей оси есть 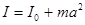. Здесь а - расстояние между осями.

Таким образом, зная момент инерции относительно оси, проходящей через центр масс, сразу находим момент инерции относительно любой другой оси.

Для доказательства рассмотрим две оси, ось z -обозначим О - совпадает с центром масс, и О¢ проходящую через т. (x₀ y₀). Расстояние между осями

.

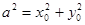Пусть частица с массой тела Dm_i имеет координаты (x_i , y_i).

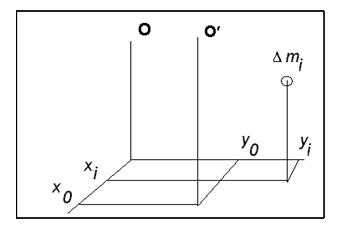
РИС. 3-21

Момент инерции относительно оси O (по определению) имеет следующий вид:

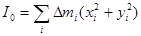
Для второй оси О¢:

. Раскроем скобки и произведем суммирование. В итоге получим искомую теорему. При этом также учитывается, что члены, соответствующие моментам сил в поле тяжести, равны нулю! Это члены вида:

для x, и аналогичный для y.

Литература к лекциям 1- 5

1. И. Е. Иродов. «Основные законы механики», 2-е изд., 1978 год.

2. С. Э. Хайкин. «Физические основы механики», 2-е изд., 1971 год.

3. С. П. Стрелков. «Механика», 3-е изд., 1975 год.

4. Берклеевский курс физики: Ч.Киттель, У.Найт, М.Рудерман «Механика», 1971 г.

5. А. В. Астахов. «Механика. Кинетическая теория материи» (Курс физики, т. 1),
1977 г.

6. Д. В. Сивухин. «Общий курс физики», т.1. Механика, Москва, 1974 г.

5 Лекция 5

Дата добавления: 2014-01-20