Винтовые поверхности. Прямой и наклонный геликоид

Поверхности вращения. Конус. Цилиндр. Сфера. Тор. Эллипсоид. Параболоид. Гиперболоид.

ЛЕКЦИЯ 5 (2 часть)

ТЕМА:

1. Поверхности вращения.

Поверхности вращения – поверхность, получаемая при вращении образующей линии вокруг неподвижной оси, называемой осью вращения (Рис.13).

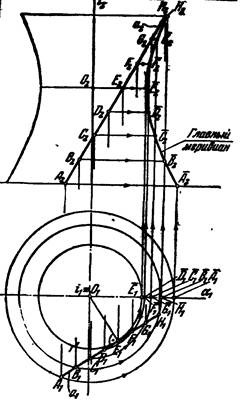Каждая точка образующей описывает при вращении окружность с центром на оси i – она называется параллелью. Наибольшая параллель – экватор, наименьшая параллель – горло. Касательные, проведенные к ним, параллельны оси вращения. Эти окружности проецируются на одну из плоскостей в виде окружностей очертания

(очерка).

Плоскости, проходящими через ось вращения, называются меридиональными плоскостями. Кривые линии, получаемые в сечении ими, называются меридианами. Плоскость, проходящая через ось i перпендикулярно П1 и параллельно П2, называется плоскостью главного меридиана и тогда главный меридиан проецируется на П2 в натуральную величину.

Рис. 13

Теорема: При вращении плоской или пространственной алгебраической кривой n –го порядка вокруг произвольной оси образуется алгебраическая поверхность вращения порядка 2n.

Положение точки или прямой на поверхности определяется при помощи параллели (или прямолинейной образующей в случае конуса и цилиндра), проходящей через эту точку.

Тор образуется при вращении окружности вокруг оси, расположенной в плоскости окружности, но не проходящей через ее центр. Различают:

Лекция 5 –8

1. Открытый тор или круговое кольцо (Рис. 14).

2. Закрытый тор (или замкнутый) (Рис. 15).

3. Самопересекающийся тор (Рис. 16)

Рис. 14 Рис. 15 Рис. 16

При вращении кривой второго порядка вокруг своей оси образуется поверхность второго порядка. Возможны следующие типы:

1. Сфера образуется при вращении окружности вокруг ее диаметра (рис.17).

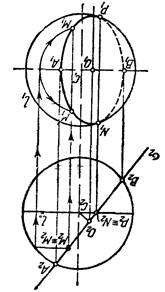
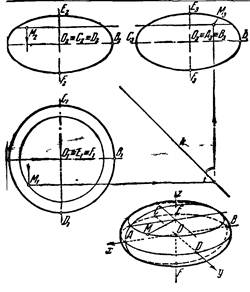
Рис. 17 Рис. 18

7. Эллипсоид вращения образуется при вращении эллипса вокруг большой оси - вытянутый эллипсоид (Рис. 18), вокруг малой оси – сжатый эллипсоид. На чертеже

показано построение проекций точки М, принадлежащей поверхности эллипсоида.

Лекция 5 –9

8. Параболоид вращения образуется при вращении параболы вокруг его оси.

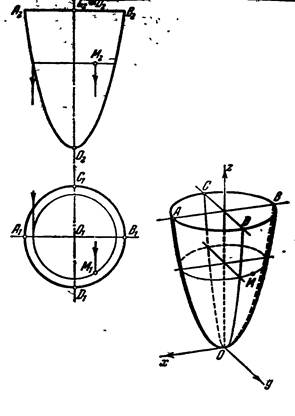
Рис. 19

8. Однополостный гиперболоид вращения образуется при вращении гиперболы вокруг ее мнимой оси oz (Рис. 20). Эта поверхность является также линейчатой поверхностью.

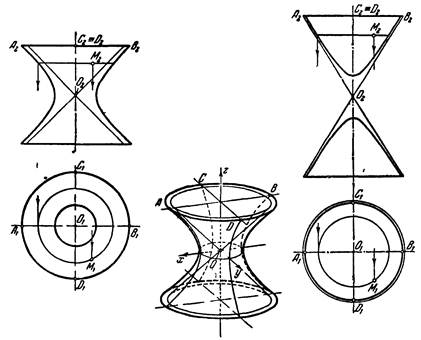
Рис. 20 Рис.21

Лекция 5-10

9. Двуполостный гиперболоид образуется при вращении гиперболы вокруг ее действительной оси oz (рис. 21).

10. Конус вращения.

11. Цилиндр вращения.

2. Винтовые поверхности. Прямой и наклонный геликоид.

Винтовая поверхность образуется при винтовом движении произвольной кривой L. Винтовое движение – это одновременное движение точки вращательное вокруг оси I и поступательное, параллельно этой же оси. Если образующая – прямая, то винтовая поверхность относится к линейчатым.

На винтовой поверхности лежат два семейства линий: образующих (прямые или кривые) и направляющих винтовых линий.

Сечения поверхности плоскостями, проходящими через ее ось, называются меридианами, а сечения плоскостями, перпендикулярно к оси, - нормальными сечениями.

Наибольшее значение в технике получили линейчатые поверхности винтовые, или геликоиды, или еще одно название – поверхности с направляющим конусом.

Поверхность может быть закрытой или открытой в зависимости от того, пересекает образующая L винтовую ось I или не пересекает.

Прямой геликоид (Рис.6)образуется прямолинейной образующей, которая, пересекая неподвижную ось I геликоида под прямым углом, вращается около этой оси и в то же время смещается вдоль нее на расстояние, пропорциональное углу поворота. Эта поверхность – закрытая.

Поступательное перемещение образующей за время одного полного оборота вокруг оси равно шагу h геликоида. Каждая прямолинейная образующая L поверхности, пересекая ось I в некоторой точке, разделяется этой точкой на два луча, каждый из которых образует свою полость поверхности. Итак, образующая l прямого геликоида движется по двум направляющим: оси и винтовой линии, оставаясь параллельной некоторой плоскости перпендикулярно, принимаемой обычно за плоскость П1.

Наклонный геликоид или архимедов отличается от прямого тем, что его прямолинейная образующая пересекает ось под некоторым заданным углом, не равным 90 градусов (Рис.7).

Образующая геликоида, пересекая при движении две направляющие: ось и винтовую линию на цилиндре, остается параллельной образующим некоторого конуса вращения с вершиной S, имеющего общую ось с винтовой линией и угол между образующей и осью, равный заданному углу. Этот конус называется направляющим конусом и с его помощью на чертеже, возможно определить угол наклона проекции любой образующей поверхности.

Построение поверхности начнем с построения горизонтальной и фронтальной проекции направляющей винтовой линии, затем разбиваем ее на 12 равных частей, начиная с горизонтальной проекции. Далее, строится направляющий конус с заданным углом при вершине S. На нем строятся образующие (те же 12, что и на винтовой линии). И параллельно соответствующим образующим конуса проводим образующие геликоида через отмеченные точки на винтовой линии.

Очертание геликоида во фронтальной проекции получается как огибающая линия семейства прямолинейных образующих. В сечении геликоида плоскостью, перпендикулярно его оси – нормальное сечение - получается спираль Архимеда.

Очертание поверхности наклонного геликоида на фронтальной плоскости получается проведением касательных к проекции двух направляющих винтовых линий. Такое

Лекция 5 –11

построение является приближенным, так как на самом деле очертание поверхности наклонного геликоида будет криволинейным. Тело, ограниченное цилиндрическими и винтовыми поверхностями, называется винтом.

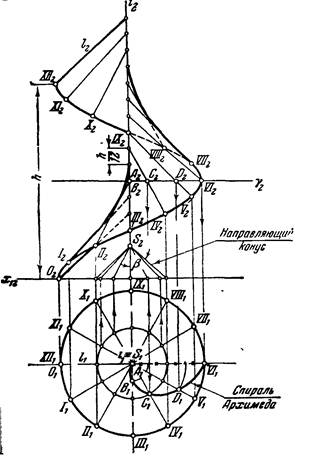
Рис. 22 Рис. 23

Дата добавления: 2014-01-20