Деревья. Определение.Ребро (xi, xj) графа G называется мостом, если в графе, полученном после удаления этого ребра

Определение. Ребро (x_i, x_j) графа G называется мостом, если в графе, полученном после удаления этого ребра, вершины x_i и x_j оказываются несвязанными.

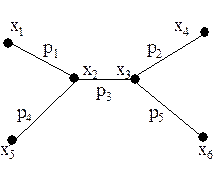Примером моста служит любое ребро графа, изображённого на рисунке 20.

Рис. 20.

Определение. Матрицей инциденций графа G = (Х, Г) с n вершинами Х = { х ₁, х ₂, …, х_n } и m рёбрами Г = { р ₁, …, р_m ½ p_k = (x_i, x_j, n)} называется прямоугольная n ´ m матрица А = ú÷ а_ij ú÷ с элементами

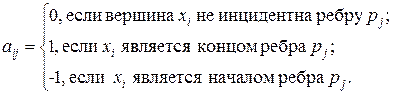
У неориентированных рёбер обоим концам соответствует 1.

Пример. Матрица инциденций графа, изображённого на рисунке 20, имеет вид:

.

В каждом столбце матрицы должны быть два ненулевых элемента, если ребро не является петлей. В строке матрицы, соответствующей изолированной вершине, нет ненулевых элементов. Матрица инциденций задает граф однозначно.

Определение. Граф называется деревом, если он связный и не содержит циклов.

Граф, состоящий из одной изолированной вершины, также является деревом. Вершина дерева, степень которой равна единице, называется висячей. Всякое ребро в дереве является мостом. Для каждой пары вершин дерева существует единственный путь, соединяющий их.

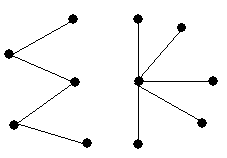
Определение. Лесом называется несвязный граф, представляющий объединение деревьев.

·

· ·

·

· ·

Рис. 21. а) дерево б) лес

При доказательстве основной теоремы о деревьях используются следующие леммы.

Лемма 1. Если G связный граф, то при добавлении к нему любого ребра, соединяющего вершины графа, в полученном графе будет простой цикл (проходящий по всем вершинам, кроме последней, в точности один раз).

Лемма 2. Граф из n вершин и m рёбер содержит не менее n - m связных компонент, а если в этом графе нет циклов, он содержит ровно n - m связных компонент.

Теорема. Пусть G граф с n вершинами и m рёбрами, тогда следующие условия эквивалентны:

1) G - дерево;

2) любые две вершины G связаны ровно одной простой цепью (путем без повторяющихся вершин и рёбер);

3) G не содержит циклов и m = n - 1;

4) G связный граф и m = n - 1;

5) G - связный граф, но при удалении любого ребра становится несвязным;

6) G не содержит циклов, но при добавлении любого нового ребра соединяющего вершины этого графа, появляется цикл.

Дата добавления: 2014-01-20