Расположение плоскости в пространстве

Способы задания плоскости

Проецирование плоскости

Плоскость является простейшей поверхностью. Плоскость безгранична. Она делит пространство на две части. Представить плоскость можно множеством точек, но любые три точки, не лежащие на одной прямой, однозначно определяют положение какой-либо плоскости в пространстве. Через точки можно провести прямые, принадлежащие данной плоскости, прямые могут в совокупности составлять некоторую плоскую фигуру. Поэтому положение плоскости в пространстве определяется положением задающих ее элементов – точек, прямых, плоских фигур. В начертательной геометрии для изображения (задания) плоскости на эпюре достаточно указать проекции:

1) плоской фигуры (рис. 28, а);

2) прямой и не принадлежащей ей точки (рис. 28, б);

3) двух пересекающихся прямых (рис. 28, в);

4) трех точек, не принадлежащих одной прямой (рис. 28, г);

5) двух параллельных прямых (рис. 28, д);

Всегда можно перейти от одного вида задания плоскости к любому другому. Например, на рис. 28, г, проведя через точки А и В прямую, можно получить задание плоскости, представленное на рис. 28, б. От него можно получить способ задания точки плоской фигурой, если соединить точки А и В с точкой С. Если на рис. 28, б провести через точку А прямую, параллельную прямой b, то получится способ задания плоскости параллельными прямыми, представленный на рис. 28, д и т. д.

а б в г д

Рис. 28

Более наглядно плоскость может быть изображена при помощи прямых, по которым она пересекает плоскости проекций (рис. 29). Такой способ задания плоскости называют задание плоскости следами. На рис. 29 следы плоскости пересекаются на оси проекций, следовательно, плоскость S тоже пересекает эту ось.

В данном случае фронтальная проекция плоскости определяется как линия пересечения плоскости S с фронтальной плоскостью проекций S₂. Горизонтальная проекция плоскости S – S₁. Угол между следами S₁ и S₂ на эпюре Монжа всегда больше угла между этими следами в пространстве.

Этот способ задания плоскости применяется достаточно часто при решении задач начертательной геометрии в случаях, когда плоскость имеет вспомогательное значение.

Рис. 29

Возможны следующие положения плоскости относительно плоскостей проекций П ₁, П ₂, П ₃:

1) плоскость не перпендикулярна ни к одной из плоскостей проекций;

2) плоскость перпендикулярна лишь к одной из них;

3) плоскость перпендикулярна одновременно к двум плоскостям проекций.

Плоскости положений 2 и 3 называют плоскостями частного положения.

Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего положения. Углы наклона к плоскостям проекций произвольные, но отличные от 0 и 90°. Плоская фигура, принадлежащая плоскости общего положения, проецируется на все три плоскости проекций с искажением. Плоскости общего положения могут быть заданы любым способом и представлены на рис. 28 и 29, кроме случаев на рис. 28, а, в.

Плоскость общего положения пересекает каждую из осей координат – x, y, z. Следы такой плоскости никогда не перпендикулярны к этим осям. Если следы плоскости общего положения образуют с осью проекций одинаковые углы, то это означает, что заданная плоскость наклонена к обеим плоскостям проекций под одинаковыми углами.

Другие примеры плоскостей общего положения приведены на рис. 30.

Плоскость, перпендикулярную к одной плоскости проекций, называют проецирующей. При этом различают:

а) горизонтально-проецирующую плоскость;

б) фронтально-проецирующую;

в) профильно-проецирующую.

Пример дан на рис. 31, плоскость задана треугольником АВС. Горизонтальная проекция треугольника представляет собой отрезок прямой линии, значит, заданная плоскость является горизонтально-проецирующей плоскостью.

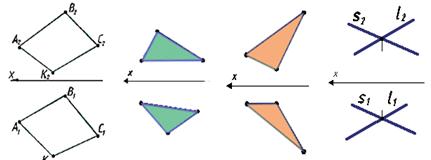
Рис. 30

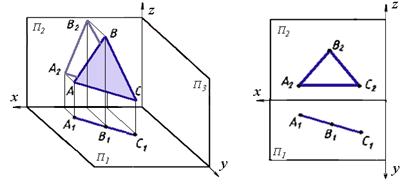
Рис. 31

Следовательно, можно сделать вывод, что если одна из проекций плоскости есть отрезок прямой линии на какой-либо плоскости проекций, то заданная плоскость перпендикулярна этой плоскости проекций. На рис. 31 треугольник АВС проецируется на фронтальную и профильную плоскости проекций с искажением.

Любые геометрические фигуры, расположенные в таких плоскостях, проецируются на перпендикулярные им плоскости проекций в виде прямых линий. Проецирующие плоскости на эпюре обычно задаются линиями их пересечения с плоскостями проекций – следами. На рис. 32 а, в изображены соответственно фронтально- и горизонтально-проецирующие плоскости, заданные треугольниками. На рис. 32, б изображена плоскость общего положения, заданная двумя параллельными прямыми.

а б в

Рис. 32

Плоскость, перпендикулярную двум плоскостям проекций называют плоскостью уровня, поскольку при таком положении плоскость становится в положение, параллельное третьей плоскости проекций. При этом различают плоскости уровня:

а) горизонтальную;

б) фронтальную;

в) профильную.

Соответственно горизонтальной плоскостью уровня называют плоскость, параллельную горизонтальной плоскости проекций; фронтальной уровня – плоскость, параллельную фронтальной плоскости проекций; профильной плоскостью уровня – плоскость, параллельную профильной плоскости проекций.

Отличительной особенностью плоскостей уровня является то, что на комплексном чертеже две проекции имеют вид прямой, расположенной под прямым углом к линиям связи, а третья проекция дает изображение всех геометрических элементов, лежащих в этой плоскости, в натуральную величину и без искажения.

Рис. 33

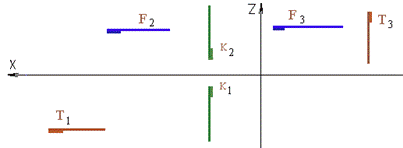
Рис. 34

На рис. 33 даны изображения плоскостей различного положения, из которых три плоскости F, K, T являются плоскостями уровня – горизонтальной, профильной и фронтальной соответственно.

На эпюре рис. 34 представлены проекции трех плоскостей уровня, наглядное изображение которых дано на рис. 33. Горизонтальная плоскость уровня F параллельна горизонтальной плоскости проекций, следовательно, она проецируется на эту плоскость без искажения. На оставшиеся две плоскости проекций плоскость F проецируется в виде прямых линий. На фронтальной плоскости проекций эта прямая параллельна координатной оси х, на профильной – параллельна оси y, обе же эти проекции перпендикулярны координатной оси z.

Аналогично в виде прямых линий плоскость Т проецируется на горизонтальную и профильную плоскости проекций, плоскость К – на горизонтальную и фронтальную.

При изображении плоскостей, заданных следами, на проекциях обычно выполняют небольшое утолщение для удобства распознавания чертежей.

Дата добавления: 2014-01-20