
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическое решение игры
|
|
|
|
В случае, когда число чистых стратегий одного из игроков (скажем, первого) равно двум, возможно геометрическое решение игры, то есть нахождение её цены и смешанных стратегий каждого игрока.
Рассмотрим идею этого решения на случае n = m =2, когда платежная матрица имеет вид:
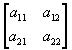 .
.
Пусть первый игрок применяет смешанную стратегию с pi = p. Тогда p2 =1- p, так как должно быть p1 + p2 =1.
Рассмотрим прямоугольную систему координат, где по оси абсцисс откладывается величина p (она занимает отрезок 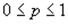 ), а по оси ординат -– величина среднего выигрыша первого игрока.
), а по оси ординат -– величина среднего выигрыша первого игрока.
Пусть второй игрок выбирает ход j =1. Тогда средний выигрыш первого игрока будет равен:
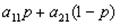 ,
,
что является отрезком прямой, соединяющей точки (a21,0) и (a11,1). Если второй игрок выбирает ход j =2, то средний выигрыш первого игрока будет равен:
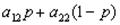 ,
,
что является отрезком прямой, соединяющей точки (a22,0) и (a12,1).
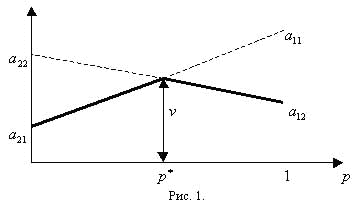
Минимальный выигрыш первого игрока представляет собой минимальное значение из ординат этих двух прямых и на рисунке он изображен жирной линией. Из рисунка видно, что максимальное значение этого минимального выигрыша определяется точкой пересечения этих двух отрезков:
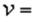
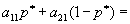
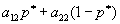
и оптимальная смешанная стратегия первого игрока есть (p*, 1- p*).
Аналогично, максимальный проигрыш второго игрока определяется максимальным значением из ординат этих двух прямых и на рисунке он изображен штриховой линией. Легко видеть, что минимальное значение этого максимального проигрыша также равно v. Смешанная стратегия второго игрока есть (q*, 1- q*), где q* находится из того условия, чтобы при любом ходе первого игрока проигрыш второго был бы равен одной и той же величине:
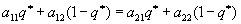
и равен также v.
Таким образом, можно найти и цену игры, и оптимальные смешанные стратегии каждого игрока.
На рисунке 1. приведен лишь самый интересный и стандартный случай. Возможны и другие варианты, два из которых приведены ниже:
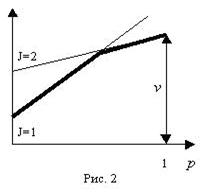
 В варианте, приведенном на рис. 2, оптимальной для первого игрока является чистая стратегия с p=1, то есть первый игрок всегда должен выбирать первый ход; для второго игрока оптимальным является выбор второго хода, то есть i=1, j=2 является седловой точкой платежной матрицы.
В варианте, приведенном на рис. 2, оптимальной для первого игрока является чистая стратегия с p=1, то есть первый игрок всегда должен выбирать первый ход; для второго игрока оптимальным является выбор второго хода, то есть i=1, j=2 является седловой точкой платежной матрицы.
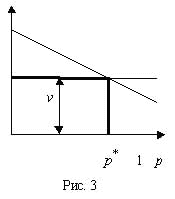
В ситуации, приведённой на рис. 3, есть целый отрезок оптимальных значений p - [0, p*], то есть оптимальная смешанная стратегия неоднозначна.
Эта методика легко переносится на случай, когда n =2, а m >2. Тогда платежная матрица имеет вид:
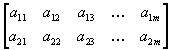
необходимо нарисовать m отрезков прямых:
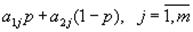 ,
,
соединяющих точки (a2j,0) и (a1j,1). Затем нужно построить ломаную линию, соответствующую минимальному значению ординат всех этих отрезков. Максимальное значение этой ломаной и даст значение цены игры v. Оптимальное значение p определится как точка пересечения этих прямых, она даст значение v.
Рассмотрим это на примере. Пусть платежная матрица имеет вид:
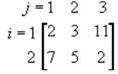 .
.
Тогда необходимо построить три отрезка прямых:
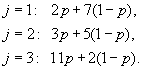
Они изображены на рис. 4, где также жирной линией выделен минимальный выигрыш первого игрока:
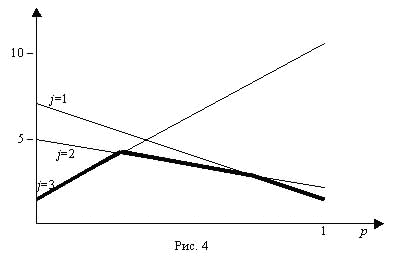
Легко видеть, что максимальное значение этого минимального выигрыша определяется пересечением прямых, соответствующих j =2 и j =3, то есть p* определяется из условия:
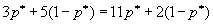 ,
,
откуда следует, что p* =3/11, так что оптимальная смешанная стратегия первого игрока есть (5/11, 8/11).
Цена игры:  .
.
Что касается второго игрока, то в образовании цены игры участвуют только j =2 и j =3. Поэтому ход j =1 он вообще не должен делать; считая, что 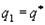 ,
, 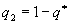 , получим:
, получим:
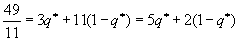 ,
,
то есть как при первом, так и при втором ходе первого игрока проигрыш второго должен быть равен v. Отсюда получаем, что q* =9/11, то есть оптимальная смешанная стратегия второго игрока есть (0, 9/11, 2/11).
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!