Логарифмический частотный критерий

Логарифмический критерий – это частотный критерий, позволяющий судить об устойчивости замкнутой САУ по виду логарифмической характеристики разомкнутой системы. Этот критерий основан на однозначной связи ЛФЧХ и АФЧХ систем автоматического управления. При этом рассматриваются САУ, базирующиеся на использовании устойчивых разомкнутых систем. Кроме того, рассматриваются системы с астатизмом не выше второго порядка.

Как следует из критерия устойчивости Найквиста в устойчивых САУ фазовый сдвиг может достигать значения только при модулях комплексной передаточной функции, меньшем чем единица. Это позволяет легко определить устойчивость по виду ЛАЧХ и ЛФЧХ.

Формулировка критерия: для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы в диапазоне частот, где ЛАЧХ разомкнутой системы 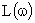больше нуля число переходов фазовой характеристики прямой 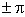снизу верх превышало на 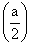число переходов сверху вниз, где а – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

В частном случае для устойчивой разомкнутой системы (а=0) необходимым и достаточным условием замкнутой системы является необходимость выполнения следующего условия. В диапазоне частот, где , фазовая частотная характеристика не должна пересекать прямой 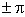, или пересекать ее одинаковое число раз снизу вверх и сверху вниз.

Рис. 6. ЛФЧХ устойчивой и неустойчивой САУ

Критическим значением коэффициента преобразования называется такое его значение, при котором АФЧХ проходит через точку (-1, j0) и система находится на границе устойчивости.

Запасом по модулю называется величина в децибеллах, на которую нужно изменить коэффициент преобразования САУ, чтобы привести ее к границе устойчивости.

,

где — частота, при которой фазовая характеристика равна .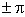

Запасом устойчивости по фазе называется угол, на который нужно повернуть амплитудно-фазовую характеристику разомкнутой системы, чтобы замкнутая САУ оказалась на границе устойчивости.

,

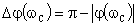где 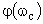– значение ФЧХ на частоте среза системы, для которой выполняется условие .

Дата добавления: 2014-01-20