Многоканальные СМО с неограниченной очередью

Пусть имеется n -канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживания – интенсивность μ. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находится в одном из состояний S₁, S₂, …, S_k, …, S_n, …, нумеруемых по числу заявок, находящихся в СМО: S₀ – в системе нет заявок (все каналы свободны), S₁ – канал занят, S₂ – заняты два канала, остальные свободны,…, S_k – занято k каналов, остальные свободны,…, S_n – заняты все n каналов (очереди нет); S_n+r – заняты все n каналов, r заявок в очереди.

Граф этой системы изображен на рисунке:

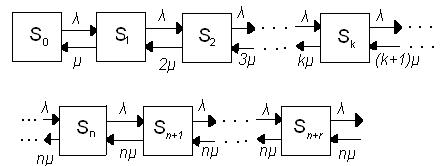
Интенсивность потока обслуживания по мере увеличения числа заявок в СМО от 0 до n увеличивается от величины μ до величины nμ, так как соответственно увеличивается число каналов обслуживания. Когда число заявок в системе больше n, интенсивность потока обслуживания сохраняется раной nμ.

В том случае, когда 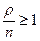, очередь неограниченно растет. Из соотношения 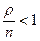следует? что предельные вероятности существуют.

, ,…,,…,,…,,…,

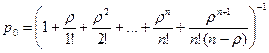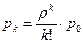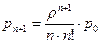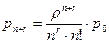
Для n -канальной СМО с неограниченной очередью можно найти:

· вероятность того, что заявка окажется в очереди:

;

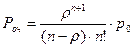· среднее число занятых каналов:

;

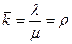· среднее число заявок в очереди:

;

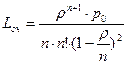· среднее число заявок в системе:

;

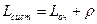· относительная величина затрат, связанная с издержками на содержание каналов обслуживания и с пребыванием в очереди заявок может быть задана например следующим образом:

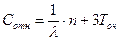
· среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе вычисляются также по формулам Литтла.

Для систем с неограниченной очередью при ρ <1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа Р_отк =0, относительная пропускная способность Q =1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, те. А = λ.

Пример. В супермаркете к расчетному центру поступает поток покупателей с интенсивностью λ= 81 человек в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя равна 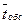=2 мин. Определить минимальное количество контролеров-кассиров n_min при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = n_min.

Решение. По условию λ= 81 (1/ч)= 81/60=1,35 (1/мин). Тогда

.

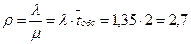Очередь не будет возрастать до бесконечности при условии, что ρ / n <1, т.е. при n > ρ =2,7. Таким образом, минимальное число кассиров n_min =3.

Найдем характеристики СМО при n =3. Вероятность того, что в центре расчета будет очередь:

.

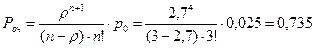(Вычисление предельных вероятностей опускаем, как заранее вычисленные, p₀ = 0,025); среднее число покупателей, находящихся в очереди:

;

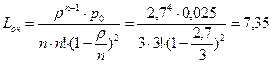среднее время ожидания в очереди:

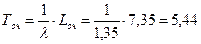мин.

Среднее число покупателей в узле расчета:

,

а среднее время нахождения покупателей в центре расчета:

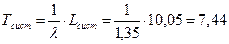мин.

Среднее число контролеров-кассиров, занятых обслуживанием покупателей:

;

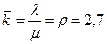коэффициент (доля) занятых обслуживанием контролеров-кассиров:

.

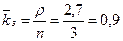Абсолютная пропускная способность узла расчета А =1,35 (1/мин), или 81 (1/час), т.е. 81 покупатель в час.

Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.

Дата добавления: 2014-01-20