Принцип относительности и преобразования Галилея

Лекция 7. Элементы релятивистской механики.

[1] гл 7

План лекции

1. Принцип относительности и преобразования Галилея.

2. Постулаты специальной теории относительности.

3. Преобразования Лоренца и следствия из них.

4. Основной закон релятивистской динамики. Закон взаимосвязи массы и энергии.

Галилей установил, что законы механики во всех ИСО имеют одинаковую форму. Для доказательства этого рассмотрим две ИСО: условно неподвижную xyz и движущуюся равномерно прямолинейно со скоростью относительно оси ОX первой системы x¢y¢z¢.

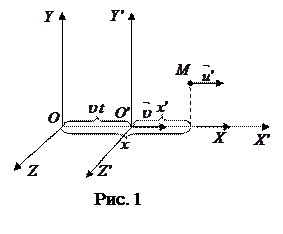В системе К ¢ точка М движется со скоростью 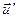относительно К¢. Положение точки М в К определяют координаты (x,y,z), в К¢ - (x¢,y¢,z¢).

Если отсчет времени начать с того момента, когда начала координат О и О¢ совпадают, то преобразования, описывающие переход от одной ИСО к другой, следующие:

- преобразования Галилея

В классической механике предполагается, что ход времени не зависит от относительного движения СО, поэтому к преобразованиям координат добавлено соотношение t=t¢.

Записанные соотношения справедливы только при .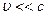

Продифференцируем их по времени

или ,

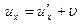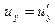или ,

или .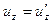

Полученные три скалярные соотношения эквивалентны следующему векторному соотношению:

,

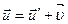где 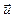- скорость точки М относительно СО xyz. Это соотношение представляет собой правило сложения скоростей в классической механике. Продифференцируем его по времени:

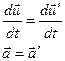
Т.к. в классической механике масса не зависит от скорости,

.

Т.о. очевидно, что и второй закон Ньютона инвариантны относительно преобразований Галилея. Подобный анализ можно провести и для других законов механики и получить такой же результат.

Т.о. уравнения (или законы) механики не изменяются (инвариантны) при переходе от одной ИСО к другой.

Принцип относительности Галилея: все механические явления протекают во всех ИСО одинаково.

Практически это проявляется в том, что никакими механическими опытами, проведенными в пределах данной ИСО, невозможно установить покоится данная ИСО или движется равномерно прямолинейно.

Дата добавления: 2014-01-20