Кинематика ламинарного потока

Ламинарным (от лат. lamina — пластинка, полоска) называется ровное, спокойное, слоистое течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть без беспорядочных быстрых изменений скорости и давления). Ламинарное течение является устойчивым, так как при случайном возмущении картина течения вскоре восстанавливается.

С примером ламинарного течения Вы уже познакомились, наблюдая в лотке Хил Шоу траектории обтекания различных моделей: окрашенные струйки воды медленно и степенно огибали препятствия, нигде не пересекая друг друга и не толкаясь, как бы тесно им не было в узких местах. Ламинарное течение является устойчивым до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное.

Осборн Рей­нольдс (Osborne Reynolds; 1842–​1912), ан­глий­ский ин­же­нер и фи­зик. Ро­дил­ся в Бел­фа­сте в се­мье свя­щен­но­слу­жителя. С 18 лет ра­бо­тал в ме­ха­ни­че­ской ма­стер­ской, по­сту­пил в Кембриджский уни­вер­си­тет, где изу­чал ма­те­ма­ти­ку и ме­ха­ни­ку. Окон­чил уни­вер­си­тет в 1867 г. В 1868–​1905 гг. — про­фес­сор ка­фед­ры стро­и­тель­ной ме­ха­ни­ки Ман­че­с­тер­ско­го уни­вер­си­те­та. С 1888 г. воз­глав­лял Витвор­тов­скую ин­же­нер­ную ла­бо­ра­то­рию. Ра­бо­ты Рейнольд­са по­свя­ще­ны ме­ха­ни­ке, гид­ро­ди­на­ми­ке, теп­ло­те, элек­три­че­ству, маг­не­тиз­му. В 1883 г. Рей­нольдс уста­но­вил, что ла­ми­нар­ное те­че­ние пе­ре­хо­дит в тур­бу­лент­ное, ко­гда вве­ден­ная им безразмерная ве­ли­чи­на (чис­ло Рей­нольд­са) пре­вы­ша­ет кри­ти­че­ское зна­че­ние.

Для течения жидкости внутри круглых труб число Рейнольдса вычисляют по формуле:

(27)

где 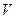- средняя скорость, d - внутренний диаметр трубы, 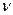- кинематическая вязкость.

Критическое число Рейнольдса для круглых труб равно 2300. При числах, меньших 2300, наблюдается устойчивое ламинарное течение.

Ламинарное течение внутри круглой трубы изучено очень подробно, основные закономерности ламинарного течения удалось установить аналитически.

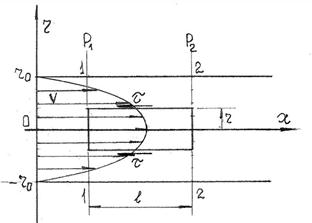Выделим внутри горизонтальной трубы диаметром 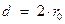соосный цилиндр радиуса 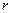и длиной .

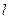На выделенный объём жидкости действуют следующие силы:

- в сечении 1-1 сила давления, равная ;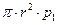

- в сечении 2-2 сила давления, равная ;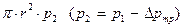

- вдоль боковой поверхности выделенного цилиндра поверхностная сила сопротивления, вызванная касательными напряжениями :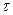

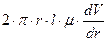
где касательное напряжение 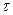для ньютоновской жидкости прямо пропорционально градиенту поперечной скорости течения:

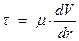(28)

Из уравнения равновесия сил следует:

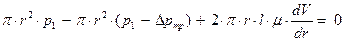(29)

Или

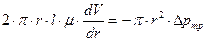(30)

Уравнение (30) можно переписать:

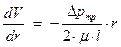(31)

Интегрируем уравнение (31), полагая, что вдоль стенки трубы (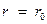) скорость равна нулю:

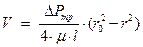(32)

Мы видим, что распределение скорости в круглом трубопроводе при ламинарном течении имеет параболический вид, а максимальное значение скорости достигается на оси трубы и равно

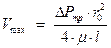(33)

Распределение скорости при ламинарном течении в круглой трубе можно выразить и так:

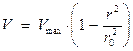(34)

Используя уравнения (2) и (32), можно вычислить расход в трубопроводе круглого сечения при ламинарном режиме:

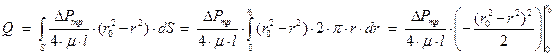(35)

Подставив значения верхнего и нижнего пределов интегрирования получаем уравнение расхода:

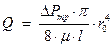(36)

Среднее значение скорости определим по формулам (1) и (36):

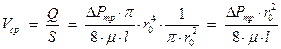(37)

Среднее и максимальное значения скорости отличаются в два раза (см. формулы (24) и (28):

(38)

Вычислим коэффициент Кориолиса для ламинарного режима. Используем для этого уравнения (10,12 и 13).

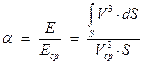(40)

В уравнении (40) используем соотношения (38) и (34):

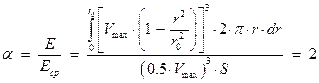(41)

Дата добавления: 2014-01-20